Петр Талантов - 0,05. Доказательная медицина от магии до поисков бессмертия

Лишь на следующий год Дженнеру удалось заручиться поддержкой нескольких влиятельных врачей, которые стали активно продвигать новый метод. Это позволило провести масштабное исследование, подтвердившее предварительные выводы. Вакцинация стала распространяться по Англии и уже на следующий год достигла других европейских стран. К 1821 году, через сто лет после бостонской эпидемии, вакцинация от оспы стала обязательной в Норвегии, Швеции, Дании и Баварии, а в 1853 году – и в Соединенном Королевстве. Постепенно она полностью вытеснила опасную инокуляцию. Последняя была запрещена сначала в Великобритании, а затем и в других развитых странах.

К 50-м годам XX века был разработан метод массового производства противооспенной вакцины. К этому времени оспа уже была почти полностью истреблена в Европе и Северной Америке, но в развивающихся странах ситуация оставалась катастрофической – ежегодно от оспы погибало до двух миллионов людей.

В 1966 году Всемирная организация здравоохранения (ВОЗ) начала кампанию по полному искоренению оспы. Возможной ее сделал выдающийся советский вирусолог Виктор Жданов. Еще в 1958 году он предложил и обосновал эту программу и с тех пор без устали убеждал скептически настроенную ВОЗ в ее целесообразности и реалистичности. Благодаря объединенным усилиям многих стран, сотням тысяч доз вакцины, произведенных в США и СССР, а также скоординированным усилиям множества организаций и правительств команде под руководством эпидемиолога Дональда Хендерсона удалось сделать то, что еще недавно казалось невозможным. В 1977 году в Судане был зарегистрирован последний случай натуральной оспы. А 9 декабря 1979 года ВОЗ объявила, что болезнь окончательно уничтожена. Так оспа стала первым и пока единственным заболеванием человека, которое удалось полностью искоренить.

Если вы родились после 1982 года, то на вашем плече нет характерного шрама [92] Не путайте со шрамами от БЦЖ, которые, в отличие от оставленного противооспенной прививкой, меньше размером, имеют гладкую поверхность и которых может быть больше одного. от противооспенной прививки. Скорее всего, его не будет и у ваших детей и внуков. Хотелось бы верить, что эти шрамы – последнее напоминание о долгой и драматичной истории, развязка которой началась в тот день, когда преподобный Мэзер и доктор Бойлстон решили использовать числа для решения медицинской проблемы.

К началу XIX века физики и астрономы стали уделять внимание факту, которому раньше не придавали большого значения: одни и те же измерения, например замеры координат небесных тел, никогда не давали в точности тот же результат. Сначала эти расхождения игнорировали, используя одно произвольно выбранное значение. Но постепенно стало понятно, что хотя приборы становятся точнее и разброс полученных значений уменьшается, он никогда не исчезает полностью. Примерно одновременно математики Карл Фридрих Гаусс в Германии и Пьер-Симон Лаплас во Франции попытались сформулировать, как, опираясь на результаты серии измерений, вычислить то одно истинное значение, которое скрывается за ними.

Гаусс и Лаплас обнаружили, что при достаточно большом количестве измерений их результаты распределяются в соответствии с тем, что сейчас мы называем нормальным (или Гауссовым) распределением . Если построить график, разместив по оси x значения измерений, а количество измерений, при которых получено такое значение [93] Под этим мы понимаем не точно совпадающие, а приближенные значения. , – по оси y , мы получим кривую, похожую на колокол: близкие к среднему значения будут встречаться чаще всего, а чем дальше значение от среднего, тем реже оно будет встречаться.

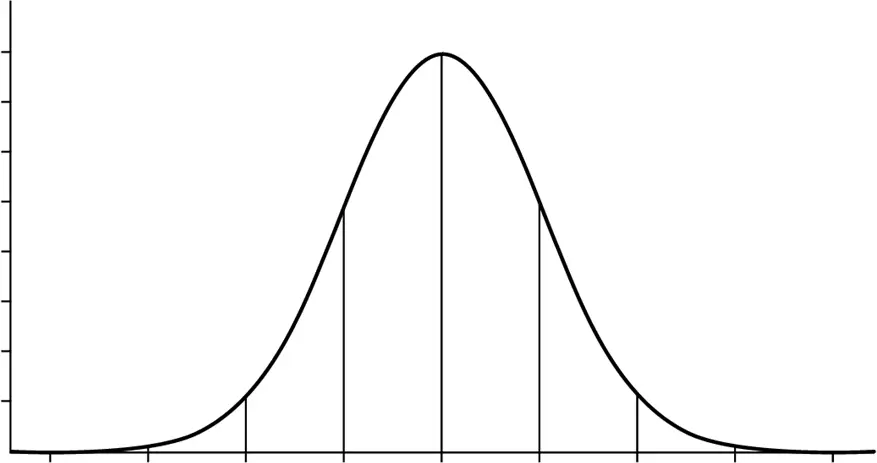
Нормальное распределение характерно для случайных процессов с результатом, складывающимся под влиянием многих независимых воздействий, каждое из которых вносит свой небольшой вклад. Нормальное распределение часто встречается в природе. Так распределены в популяции размеры живых организмов, отдельных органов, тканей, конечностей, некоторые психические и физиологические параметры, такие как коэффициент интеллекта.

Если у вас есть немного свободного времени и пять игральных кубиков, вы можете провести небольшой эксперимент – он поможет понять, почему и как это происходит. Возьмите листок бумаги и начертите оси координат. Ось х разметьте от пяти до тридцати. После каждого броска суммируйте значения выпавших сторон и добавляйте по одному делению по оси y над тем значением суммы, которое выпало. Поскольку средние значения сумм образуются бóльшим количеством комбинаций, а значит чаще, чем очень маленькие или очень большие, то средняя часть графика начнет заполняться намного быстрее.

Вам может понадобиться немало бросков перед тем, как вы увидите характерную кривую нормального распределения. Если у вас не так много времени, воспользуйтесь автоматическим сервисом, который делает то же самое – вы найдете его на сайте Academo.org [94] https://academo.org/demos/dice-roll-statistics/ . Отметьте галочкой опцию Roll automatically и наблюдайте, как по мере стремительного увеличения количества бросков ваш график все больше становится похож на колокол.

Гаусс первым использовал при расчете орбиты небесного тела представление о нормальном распределении результатов наблюдений. Рассчитав таким образом вероятности реального положения орбиты астероида Цереры, он смог достаточно точно предсказать движение небесного тела, исходя из очень небольшого количества данных. Так статистика и теория вероятностей [95] И статистика, и теория вероятностей – разделы математики. Если первый занимается анализом наблюдаемых феноменов, то второй – предсказанием их поведения на основе этого анализа. стали постепенно вытеснять царивший в экспериментальной науке детерминизм.

Детерминизм исходит из того, что все события полностью предопределены вызвавшими их причинами. Возможно, так оно и есть, но на практике мы не можем предсказать исход многих процессов в силу их высокой сложности, то есть большого количества факторов, каждый из которых вносит свой вклад.

Теоретически мы можем заранее просчитать результат броска игральных кубиков, если построим точную модель траектории их движения с учетом скоростей, угловых скоростей, отклонения осей вращения, высоты броска, сопротивления воздуха и свойств поверхности, на которую они упадут [96] Замечательный иллюзионист Николай Фомушин объяснил мне, что даже опытному фокуснику довольно сложно выбросить игральную кость нужной стороной. Теоретически это возможно, если бросать одну кость с помощью рук. Но при использовании более чем одной кости и стаканчика для перемешивания костей задача становится практически невыполнимой. . Но зачастую у нас нет возможности получить всю информацию, необходимую для построения детерминистической модели. Более того, минимальные изменения начальных данных (угла, силы, высоты) приведут к принципиальному изменению результата броска. Поэтому на практике такой подход неприменим. Зато мы можем оперировать вероятностями, которые определяем, исходя из того, как кубики вели себя в прошлом, и с их помощью предсказывать шансы на те или иные результаты в будущем.