Ирина Бодэ - Гиппократ не рад. Путеводитель в мире медицинских исследований

Аналогичную функцию медиана выполняет в статистике применительно к распределению величин. Медиана в статистике – это такое значение, которое разделяет распределение пополам, то есть половина значений распределения больше медианы, а половина – меньше (рис. 7). Мода – ещё один статистический параметр, обозначающий значение, которое встречается наиболее часто в нашей выборке.

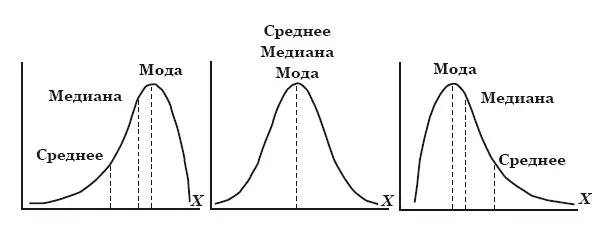
Рис. 7. Среднее, медиана и мода. Слева направо: ассимметричное распределение, нормальное распределение и ассимметричное распределение

Как видно из рис. 7, для идеального нормального распределения среднее и медиана должны совпасть (как и в случае с равнобедренным треугольником), однако если нам нужна информация о том, какое именно значение находится в середине асимметричного распределения, медиана будет гораздо предпочтительнее. Кроме медианы, существуют так называемые процентили, наиболее часто из них используются квартили, то есть 25-й и 75-й процентили. Эти показатели показывают четверть наибольших и наименьших показателей в распределении. Сама медиана считается 50-м процентилем (рис. 8).

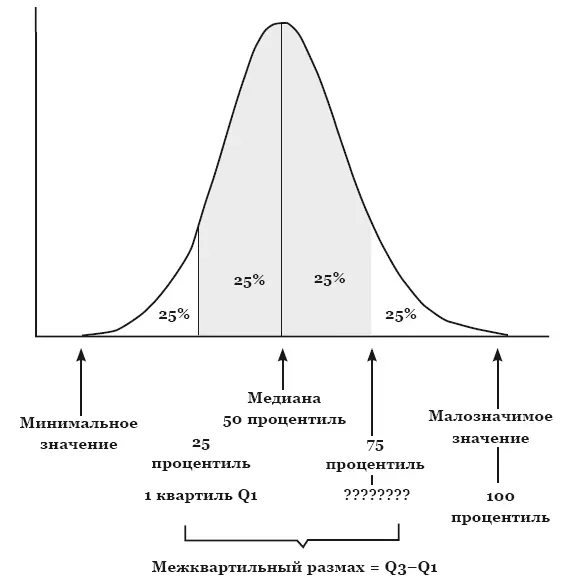
Рис. 8. Распределение с обозначенными минимальным и максимальным значениями, а также медианой и 25-м и 75-м процентилями

Итак, получается, что если наше распределение имеет вид идеальной гауссианы, мы легко можем оперировать параметрами распределения, но если распределение отличается от нормального, нам начинает не хватать среднего и СКО, необходимо вводить другие характеристики, такие как процентили и медиана.

Так как эти статистические характеристики наиболее понятны и просты, параметрические методы в статистике получили большую популярность. Практически ни одно исследование не обходится без их применения. Возраст, масса тела, рост, некоторые биохимические показатели – эти характеристики вполне соответствуют нормальному распределению, а значит, данные можно обрабатывать параметрикой. К параметрическим методам относятся, например, t-критерий Стьюдента, знакомый многим студентам, например по выполнению лабораторных по физике.

Критерий Стьюдента. Самый любимый и самый понятный! По сути он является частным случаем более сложного метода анализа, однако при изучении статистики рациональнее всегда начинать с изучения именно критерия Стьюдента. Данный метод позволяет нам сравнить, насколько отличаются две выборки друг от друга. В англоязычной литературе чаще называется просто t test (подозреваю, что это из-за сходства в написании Student [Стьюдент] и student [студент], что значительно усложняет поиск в Интернете).

Существует два типа t-теста:

• для независимых выборок, когда две сравниваемые группы никак друг от друга не зависят;

• парный (paired) для зависимых выборок, когда две сравниваемые группы зависят друг от друга.

Как правило, критерий применяется в тех случаях, когда испытуемых разделяют на две независимые группы, именно об этом мы и поговорим. Например, пациентов могут разделить на две группы: контрольную, которой дают плацебо, и ту, на которой испытывают реальные лекарства (экспериментальная группа). Таким образом, мы можем получить сразу много данных о каждой группе: какими были интересующие нас показатели (например уровень глюкозы в плазме крови) в группе плацебо до «лечения» и после? А в экспериментальной? Можно сравнить результаты исследований до начала активной фазы исследований и после. Тогда мы поймём, влияет ли как-то наше вмешательство на исследуемые параметры или нет.

Например, наше лекарство должно снижать уровень глюкозы в плазме крови. Если мы честные исследователи, то пациентов в каждую из групп, контрольную и экспериментальную, мы выбирали одинаково по тем же самым параметрам. Значит, и различий между группами по показателю содержания глюкозы в плазме крови до приёма плацебо и лекарства соответственно быть не должно. Но если наше лекарство действует лучше, чем ничего (пустышка-плацебо), значит, после лечения уровень глюкозы должен будет отличаться между группами. Так как глюкоза у нас в организме содержится в строго определённых пределах (меньше и больше определённых значений, к сожалению, означает смерть), а в норме натощак встречается в пределах примерно от 3.5 до 5.5 ммоль/л, можно заранее предположить нормальное распределение. Конечно, наше предположение никак не освобождает нас от необходимости проверки на нормальность: вдруг мы какие-то аномалии получили? Но если нормальность распределения подтверждается, можно использовать t-критерий Стьюдента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

Децентрализованная система, в которой совершение любых действий фиксируется участниками системы и подтверждается ими.

Поражение нервной системы, характеризующееся болью, мышечной слабостью, онемением, повышенной чувствительностью, потерей координации и многими другими симптомами.

Это нам пригодится при написании больших систематических обзоров или метаанализов. Подробнее об этом написано в разделе «Работающая гипотеза».

Доклинические испытания – исследования не на людях. Они проводятся для проверки конкретного вещества и его биологического действия, выбора дозировок, определения токсичности и прочих параметров. Клинические исследования – это исследования, в которых проверяются эффективность и безопасность лекарственного средства непосредственно на выборках людей. Существующие протоколы не подразумевают возможности регистрации препарата и выхода его на рынок без проведения доклинических и клинических испытаний, при этом клинические испытания нельзя проводить до проведения доклинических (что логично вытекает из названий).