Дмитрий Миронов - Компьютерная графика в дизайне

Рис. 1.3.7. Имитация цвета для монохромного индексированного изображения: а – имитация отсутствует; б – имитация цвета по методу диффузии

Имитация цвета – важный прием, использующийся не только совместно с индексированной моделью, но и с описанными в последующих разделах полноцветными моделями.

Аддитивными моделями цвета (от англ. add – складывать) называются цветовые модели, в которых световой поток со спектральным распределением, визуально воспринимающимся как нужный цвет, создается на основе операции пропорционального смешивания света, излучаемого тремя источниками. Схемы смешивания могут быть различными, одна из них представлена на рис. 1.3.8.

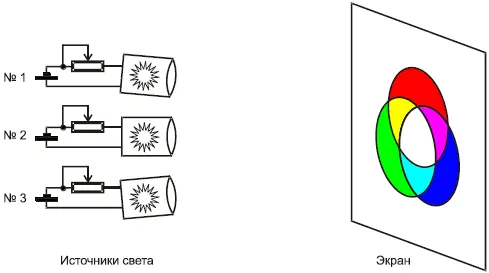
Рис. 1.3.8. Схема смешивания световых потоков в аддитивной модели цвета

Аддитивная модель цвета предполагает, что каждый из источников света имеет свое постоянное спектральное распределение, а его интенсивность регулируется.

Существуют две разновидности аддитивной модели цвета: аппаратно-зависимая и перцептивная. В аппаратно-зависимой модели цветовое пространство зависит от характеристик устройства вывода изображения (монитора, проектора). Из-за этого одно и то же изображение, представленное на основе такой модели, при воспроизведении на различных устройствах будет восприниматься визуально немного по-разному. Перцептивная модель построена с учетом особенностей зрения наблюдателя, а не технических характеристик устройства.

Название этой модели происходит от аббревиатуры, состоящей из первых букв английских названий ее базовых цветов (см. разд. 1.3.2). Красный, зеленый и синий цвета были выбраны в качестве базовых потому, что эти волновые диапазоны видимой части спектра максимально удалены друг от друга. Кроме того, они близки к диапазонам, на которые избирательно реагируют колбочки сетчатки.

Цветовое пространство модели RGB непрерывно, но принято разбивать диапазоны интенсивности свечения источников на 256 интервалов. Нулевое значение соответствует отсутствию свечения, 255 – максимальной интенсивности, которую обеспечивает источник света. На рис. 1.3.9 цветовое пространство RGB представлено в виде куба в декартовой системе координат, в которой каждая из осей соответствует интенсивности свечения одного из источников базового цвета.

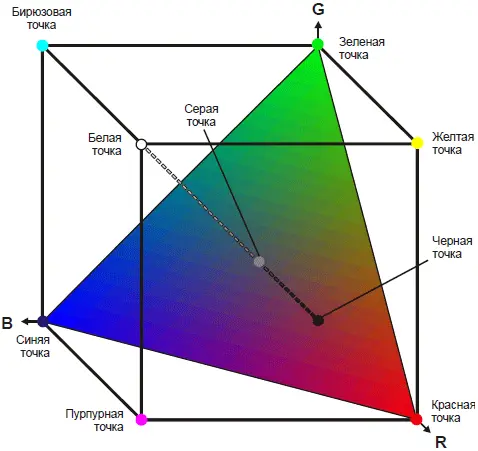
Рис. 1.3.9. Цветовое пространство модели RGB

На гранях куба, определяющего цветовое пространство, и внутри него каждой точке соответствует свой цвет. При разбиении каждой из осей цветовых координат на 256 интервалов глубина цвета модели составляет 24 бита. Это означает, что в ней имеется 2 24цветов, т. е. 16 777 216.

Примечание

В задачах, требующих высокой точности воспроизведения цвета, может устанавливаться удвоенная глубина цвета 48 битов и даже учетверенная – 96 битов. Конечно, при этом соответственно вдвое или вчетверо увеличивается объем памяти, необходимый для размещения информационной модели изображения.

Местоположение любой точки (а значит, и любого цвета) в цветовом пространстве задается тремя числами, соответствующими значениям цветовых координат. Запись этих чисел в виде RxGyBz (где x, y и z – целые числа от 0 до 255) называется формулой цвета RGB.

В цветовом пространстве RGB имеются характерные точки и линии. Формуле цвета R0G0B0 соответствует точка в начале цветовых координат и черный цвет (интенсивность излучения всех трех источников света равна нулю). Формуле цвета R255G255B255 соответствует "белая" точка, в ней интенсивность свечения всех источников максимальна. Эти две точки соединяет диагональ куба, вдоль которой расположены цвета монохроматической шкалы – оттенки черного цвета. Эти точки соответствуют ахроматическим цветам. На пересечении диагоналей куба расположена "серая" точка R127G127B127, определяющая цвет, который в компьютерной графике называется нейтральным серым.

Линии, проведенные через "черную" точку и произвольно выбранную точку куба, представляют собой монохроматические шкалы, в которых в качестве фонового цвета выступает черный, а цветом переднего плана является цвет, соответствующий выбранной точке. Линии, проведенные через "белую" точку и произвольно выбранную точку куба, представляют собой монохроматические шкалы, в которых в качестве фонового цвета выступает белый, а цветом переднего плана является цвет, соответствующий выбранной точке.

Точки, лежащие на осях цветовых координат, соответствуют оттенкам базовых цветов модели RGB. Наиболее удалены от начала координат "красная" R255G0B0, "зеленая" R0G255B0 и "синяя" R0G0B255 точки. В остальных вершинах куба располагаются точки, соответствующие дополнительным цветам модели RGB:

• бирюзовому, R0G255B255 (обозначается латинской буквой C);

• пурпурному, R255G0B255 (обозначается латинской буквой М);

• желтому, R255G255B0 (обозначается латинской буквой Y).

Отметим важный факт – дополнительные цвета цветовой модели RGB получаются при смешивании попарно в равной пропорции ее базовых цветов.

Большое значение имеет изображенный на рис. 1.3.9 треугольник цветности, представляющий собой лежащую в пределах цветового пространства часть плоскости, проходящей через «красную», «синюю» и «зеленую» точки. Принадлежащие ему точки называются точками единичного цвета. Цветностью или хроматикой цвета в компьютерной графике называется характеристика, имеющая одинаковое значение для всех оттенков одного цвета и различные значения для любой пары оттенков разных цветов.

Примечание

Напомним, что оттенки получаются из спектрально чистого цвета смешиванием его с черным или белым.

Цветность определяет, в каком месте спектра располагается цвет.

Ранее уже отмечалось, что линиям, проходящим через "черную" или "белую" точку, соответствуют шкалы оттенков одного цвета. Проведем две прямые через любую точку цветового пространства RGB (заданную точку) так, чтобы одна из них прошла через "черную" точку, а другая – через "белую". Одна из этих прямых обязательно пройдет через какую-нибудь точку треугольника цветности. Причем цвета, соответствующие этой точке единичного цвета и заданной точке, будут принадлежать одной монохромной шкале и будут являться оттенками одного и того же цвета, различающимися только яркостью и насыщенностью (содержанием черного или белого). Таким образом, в треугольнике цветности "представлены" все цвета цветовой модели, хотя и оттенками различной яркости. Это позволяет использовать треугольник цветности в качестве графического представления цветового охвата модели.