Глеб Носовский - Какой сейчас век?

Сформулируем теперь принцип затухания частот, описывающий хронологически правильный порядок "глав-поколений".

При правильной нумерации "глав-поколений" летописец, переходя от описания одного поколения к следующему, сменяет и персонажей. А именно, при описании поколений, предшествующих поколению с номером Q, он ничего не говорит о персонажах этого поколения, так как они еще не родились. Затем, при описании поколения Q, летописец именно здесь больше всего говорит о персонажах этого поколения, поскольку с ними напрямую связаны описываемые им события. Наконец, переходя к описанию последующих поколений, летописец все реже и реже упоминает о прежних персонажах, так как описывает новые события, персонажи которых вытесняют умерших.

Здесь важно подчеркнуть, что мы имеем в виду не какие-то отдельные имена, а полный резервуар всех имен, использовавшихся в поколении с номером Q.

Вкратце наша модель формулируется так. Каждое поколение рождает новые исторические лица. При смене поколений эти лица сменяются.

Несмотря на внешнюю простоту, этот принцип оказался полезен при создании метода датировки. Принцип затухания частот имеет эквивалентную переформулировку. Так как персонажи практически однозначно определяются своими полными именами (имя = персонаж), то мы будем изучать резервуар всех полных имен текста. Термин "полное" будем обычно опускать, постоянно подразумевая его. Более того, оказалось, что подавляющее большинство исторических имен являются "простыми", состоящими из одного слова. Поэтому при обработке больших исторических текстов со значительным запасом имен можно рассматривать лишь "элементарные имена – кирпичи", разбивая редкие полные имена на отдельные составляющие их слова.

Рассмотрим группу всех имен, впервые появившихся в тексте, в "главе-поколении" с номером Q. Условно назовем эти имена Q-именами, а соответствующие им персонажи Q-персонажами. Количество всех упоминаний, с кратностями, всех этих имен в данной "главе" обозначим через K(Q, Q). Подсчитаем затем, сколько раз эти же имена упомянуты в "главе" с номером Т. Получившееся число обозначим через K(Q, 7).

При этом если одно и то же имя повторяется несколько раз, то есть с кратностью, то все эти упоминания подсчитываются. Построим график, отложив по горизонтали номера "глав", а по вертикали – числа K(Q, T), где номер Q фиксирован, а Г меняется. Для каждого Q мы получаем свой график. Принцип затухания частот тогда формулируется так.

При хронологически правильной нумерации "глав-поколений" каждый график К(Q, T) должен иметь следующий вид. Слева от точки Q график равен нулю, в точке Q – абсолютный максимум графика, потом график постепенно падает, более или менее монотонно затухает (рис. 5.12).

Этот график (на рис. 5.12) мы назовем идеальным.

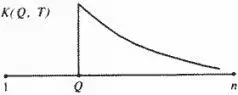
Сформулированный принцип должен быть проверен экспериментально. Если он верен и если "главы" в летописи упорядочены хронологически правильно, то все экспериментальные графики должны быть близки к идеальному. Проведенная экспериментальная проверка полностью подтвердила принцип затухания частот.

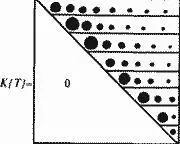
Всего нами было обработано несколько десятков больших исторических текстов. Во всех случаях, когда тексты описывают события эпохи XVI-XX веков, принцип затухания частот подтвердился. Отсюда вытекает методика хронологически правильного упорядочивания "глав-поколений" в тексте, или в наборе текстов, где этот порядок нарушен или неизвестен. Рассмотрим совокупность "глав-поколений" летописи X и занумеруем их в каком-нибудь порядке. Для каждой "главы" X(Q) подсчитаем число K(Q, T) при заданной нумерации "глав". Все числа K(Q, T), при переменных Q и Т, естественно организуются в квадратную матрицу К{T} размера n*n, где n – общее число "глав". В идеальном теоретическом случае частотная матрица К{T} имеет вид, показанный на рис. 5.13.

На рис. 5.13 ниже главной диагонали стоят нули, на главной диагонали расположен абсолютный максимум в каждой строке. Затем каждый график, в каждой строке, монотонно падает, затухает.

Оказывается, аналогичная картина затухания наблюдается и для столбцов матрицы. Это означает, что частота употребления в "главе" X(Q) имен более раннего происхождения "в среднем" тоже падает по мере удаления поколения Т, породившего эти имена, от фиксированного поколения Q.

Для оценки скорости затухания частот удобно пользоваться усредненным графиком

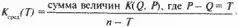
В этой формуле суммирование выполняется по всем парам (Q, Р), для которых разность Р – Q фиксирована и равна Т. Другими словами, график Ксред (T) получается усреднением матрицы К{Т} по ее диагоналям, параллельным главной. Он изображает "усредненную строку" или "усредненный столбец" частотной матрицы. Здесь Т изменяется от 0 до n – 1.

Конечно, экспериментальные графики могут не совпадать с теоретическим.

Если теперь изменить нумерацию "глав" в летописи, то изменятся и числа K(Q, T), поскольку возникает довольно сложное перераспределение "впервые появившихся имен". Следовательно, меняются частотная матрица К{T} и ее элементы. Будем менять порядок "глав" летописи с помощью различных перестановок s.

Каждый раз вычислим новую частотную матрицу K(sT), где sT – новая нумерация, соответствующая перестановке s. Будем искать такой порядок "глав" летописи, при котором все или почти все графики будут иметь вид, показанный на рис. 5.12. В этом случае экспериментальная частотная матрица K{sT} будет наиболее близка к теоретической матрице на рис. 5.13. Тот порядок "глав" летописи, при котором отклонение экспериментальной матрицы от "идеальной" будет наименьшим, и следует признать хронологически правильным и искомым.

Наш метод также позволяет датировать события. Пусть дан какой-то исторический текст Y, о котором известно только, что он рассказывает о неких событиях из эпохи (А, В), уже описанной в тексте X, разбитом на "главы-поколения", причем порядок этих "глав" в летописи X хронологически правилен. Как узнать, какое именно поколение описано в интересующем нас тексте Y? При этом мы хотим использовать только количественные характеристики текстов, не апеллируя к их смысловому содержанию, которое может быть разным или допускать сильно разнящиеся трактовки.

Ответ таков. Присоединим текст Y к совокупности "глав" хроники X, считая при этом Уновой "главой" и приписав ей какой-то номер Q. Затем установим оптимальный, хронологически правильный порядок всех "глав" получившейся "летописи". При этом мы найдем правильное место и для новой "главы" Y. В простейшем случае, построив для нее график K(Q, T), можно добиться, меняя ее положение относительно других "глав", чтобы этот график был как можно ближе к идеальному. То положение, которое Y займет среди других "глав", и следует признать за искомое. Тем самым мы датируем события, описанные в Y.