Эдвин Эбботт - Флатландия. Сферландия

Однако мы никогда не сможем доказать, что наше пространство является строго евклидовым, поскольку неизбежные ошибки наблюдения приводят к тому, что результаты измерений колеблются в узком интервале, И хотя в пределах, допускаемых точностью измерений, наше пространство, по-видимому, можно считать евклидовым, наши измерения доказывают лишь, что кривизна пространства мала, но не позволяют утверждать, что она равна нулю. В сферической и псевдосферической геометрии разность между суммой углов треугольника и двумя прямыми углами тем больше, чем больше площадь треугольников. Но даже треугольники, построенные в межзвездном пространстве для изучения параллаксов светил, исчезающе малы по сравнению с размерами самого пространства, и вопрос о том, будет ли сумма углов достаточно больших треугольников всегда равна двум прямым углам, остается открытым. Даже наши несовершенные измерения могут установить, что в реальном пространстве выполняется геометрия Лобачевского (или Римана). Например, так произойдет, если мы сумеем произвести угловые измерения с точностью до одной миллионной секунды и при этом выяснится, что сумма углов некоторого межзвездного треугольника меньше (или больше) двух прямых углов на две миллионных секунды.

Относительно реального физического пространства мы не можем с уверенностью сказать, является ли оно евклидовым или неевклидовым. Геометрия не может пролить свет па природу реального пространства. Исследование реального пространства — эмпирическая наука, в то время как геометрия представляет собой творение чистого мышления, раздел чистой математики. Говоря о чистой математике, мы имеем в виду некую совокупность гипотетических дедуктивных теорий, каждая из которых состоит из определенной системы исходных неопределяемых понятий или символов и исходных недоказываемых, но непротиворечивых допущений (обычно называемых аксиомами) и. логически выводимых из них следствий, полученных строго дедуктивными рассуждениями без обращения к интуиции. В этом смысле чистая математика представляет собой не что иное, как символическую или формальную логику. Чистая математика занимается извлечением следствий, а не приложениями. С другой стороны, естественные науки, носящие эмпирический характер и всецело зависящие от наблюдения и эксперимента, не могут достичь абсолютной точности и поэтому не могут стать строго математическими. Таким образом, достоверность геометрии зиждется лишь на необходимости, с которой ее выводы следуют из непротиворечивых посылок. Чистая математика не занимается вопросом о том, в какой мере полученные выводы применимы к материальному миру. Таким образом, геометрия, если говорить о ее приложении к реальному миру, полезна, хотя к ее выводам следует относиться с известной осторожностью.

Из того факта, что все разделы чистой математики, включая геометрию, носят строго дедуктивный характер и в действительности представляют собой не что иное, как формальную логику, следуют важные философские выводы. Они решительно опровергают Канта, который основывал всю свою философию на предполагаемой возможности образования «синтетических априорных суждений», то есть получение абсолютной истины интуитивным чистым мышлением, совершенно независимо от опыта. Для подтверждения своей точки зрения Кант ссылался на существование геометрии. Такой аргумент мог считаться неопровержимым лишь до открытия неевклидовой геометрии. Другой далеко идущий вывод сводится к следующему. Метафизические аксиомы представляют собой лишь имитацию геометрических аксиом и, подобно последним, будут отброшены. Поэтому нам представляется уместным закончить наш очерк следующими словами знаменитого немецкого математика Гильберта: «Наиболее многообещающим и значительным достижением прошлого века следует считать открытие неевклидовой геометрии».

Школьник рано знакомится с измерением отрезков, площадей и объемов. Измеряя отрезок, школьник находит его длину. Измеряя площадь фигуры, школьник разбивает ее на квадраты или прямоугольники, поскольку ему известно, что площадь прямоугольника равна произведению ширины на высоту. Измеряя объем тела, школьник разбивает его на несколько прямоугольных параллелепипедов или кубов, поскольку ему известно, что объем прямоугольного параллелепипеда равен произведению длины на ширину и на высоту. Отрезок имеет одно измерение (длину), прямоугольник — два взаимно перпендикулярных измерения (длину и ширину), прямоугольный параллелепипед — три измерения, каждое из которых перпендикулярно двум другим (длину, ширину и высоту). Изобразим единицы линейных, квадратных и кубических мер (например, сантиметр, квадратный сантиметр и кубический сантиметр) в виде отрезка AB, квадрата ABCD, сторона которого равна отрезку AB, и куба ABCDEFGH, ребро которого по длине совпадает с отрезком AB, а грань имеет размеры квадрата ABCD (рис. 1). Единичный отрезок AB можно считать состоящим из бесконечно большого числа M точек, распределенных непрерывно от одного конца A отрезка до другого конца B.

Тогда квадрат ABCD содержит M × M = M ² точек, а куб ABCDEFGH содержит M × M × M = M ³ точек [16] Буквой M здесь обозначена мощность континуума, которая не удовлетворяет неравенству N ² > N (или N ³ > N ), справедливому лишь для всех конечных чисел N > 1. Являясь величиной совсем другой природы — одним из типов бесконечности, M (хотя она и больше 1, как, впрочем, и любого другого конечного числа) подчиняется иной, менее привычной арифметике: M г = M (или M ³ = M )! — Прим. перев. . Из любой точки отрезка AB в любую другую точку того же отрезка можно перейти, двигаясь в одном фиксированном направлении, а именно в направлении отрезка AB. Аналогично из любой точки квадрата ABCD в любую другую его точку можно перейти, двигаясь вдоль двух фиксированных направлений, параллельных двум сторонам квадрата, сходящимся в одной вершине, а из любой точки куба ABCDEFGH в любую другую его точку можно попасть, двигаясь вдоль трех фиксированных направлений, параллельных трем ребрам куба, сходящимся в одной вершине (направление вперед и назад при движении вдоль любого направления мы не различаем). Таким образом, если говорить о движении, переводящем одну точку фигуры в другую, то единичный отрезок следует считать одномерным, единичный квадрат — двумерным и единичный куб — трехмерным.

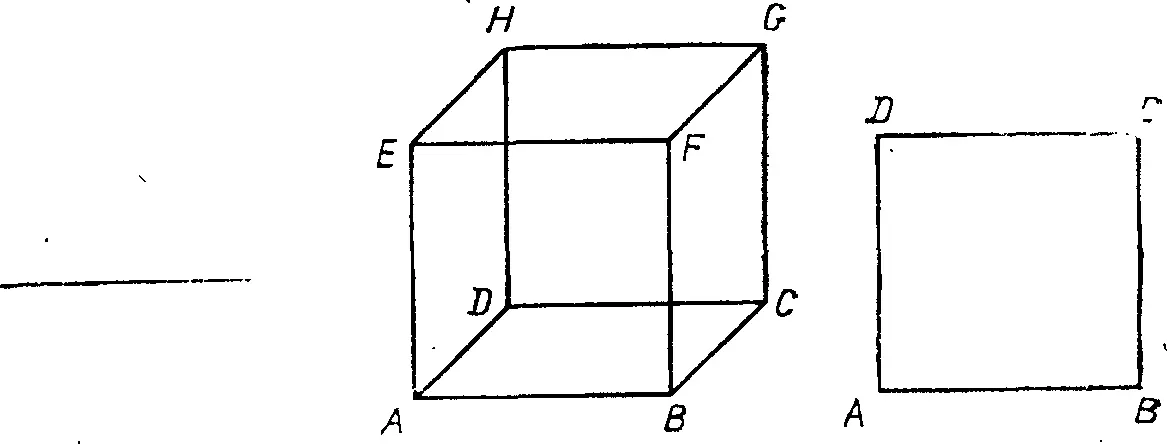
В трехмерном пространстве нет такого движения, которое нельзя было бы разложить на движение но трем взаимно перпендикулярным направлениям. На Земле нет такой точки, которой нельзя было бы достичь, двигаясь на север или на юг, на запад или восток и вверх или вниз. В комнате нет ни одной точки, до которой нельзя было бы добраться, двигаясь вдоль длины, ширины и высоты. Зрение позволяет нам воспринимать непосредственно лишь два измерения предмета (ширину и высоту), в то время как третье измерение (расстояние до предмета) мы оцениваем по мышечному усилию, необходимому для того, чтобы сфокусировать глаза на интересующем нас предмете. Мы не обладаем органом чувств, способным воспринимать четвертое измерение, перпендикулярное трем остальным измерениям. Весь человеческий опыт позволяет нам довольствоваться тремя измерениями.