Эдвин Эбботт - Флатландия. Сферландия
- Название:Флатландия. Сферландия
- Автор:
- Жанр:
- Издательство:Мир
- Год:1976
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Эдвин Эбботт - Флатландия. Сферландия краткое содержание
Книга дополнена научно-популярными статьями о четвертом измерении. Ее с интересом и пользой прочтут все любители занимательной математики.
Флатландия. Сферландия - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Но оставим опыт и обратимся к рассуждениям по аналогии. Четвертое измерение можно ввести следующим образом. Объем четырехмерного куба равен произведению длины, ширины, высоты и некоторого четвертого измерения. Чтобы вычислить объем четырехмерного прямоугольного параллелепипеда, необходимо произвести четыре линейных измерения, причем каждое в направлении, перпендикулярном трем остальным. Следовательно, четвертое измерение образует прямой угол с каждым из трех направлений, вдоль которых мы измеряем длину, ширину и высоту трехмерного прямоугольного параллелепипеда. Четырехмерный единичный куб должен иметь ребро, совпадающее с отрезком AB, грань совпадающую с квадратом ABCD, и основание, совпадающее с кубом ABCDEFGH. Четырехмерный единичный куб содержит M × M × M × M = M ⁴ точек. Перейти из одной его точки в любую другую можно, двигаясь в четырех фиксированных направлениях, параллельных четырем его ребрам, сходящимся в одной вершине.
Квадрат ABCD (рис. 1) мы получим из отрезка AB, передвинув этот отрезок со всеми его M точками на расстояние, равное 1см в направлении, перпендикулярном единственному измерению отрезка AB. Каждая точка отрезка AB при движении описывает некоторый отрезок, и, таким образом, квадрат ABCD содержит M отрезков, так же как и M ² точек. Куб ABCDEFGH мы получим из квадрата ABCD, сдвинув квадрат ABCD на расстояние, равное 1см, в направлении, перпендикулярном двум измерениям квадрата. При движении M отрезков и M ² точек квадрата опишут соответственно M квадратов и M ² отрезков. Следовательно, куб ABCDEFGH содержит M квадратов, M ² отрезков и M ³ точек. Аналогично четырехмерный единичный куб мы получим из трехмерного куба ABCDEFGH , передвинув этот куб на расстояние, равное 1см, в направлении, перпендикулярном каждому из трех измерений куба, то есть в направлении четвертого измерения. При движении M квадратов, M ² прямых и M ³ точек трехмерного куба ABCDEFGH опишут соответственно M кубов, M ² квадратов и M ³ отрезков. Следовательно, четырехмерный единичный куб содержит M кубов, M ² квадратов, M ³ отрезков и M ⁴ точек. Обратимся теперь к рассмотрению элементов, образующих границы единичных отрезков, квадратов, кубов и четырехмерных кубов. У единичного отрезка AB имеются две граничные точки («вершины»). У единичного квадрата ABCD — четыре вершины, у единичного куба ABCDEFGH — восемь вершин (по четыре от начального и конечного положения производящего квадрата), а у четырехмерного единичного куба — 16 вершин (по восемь вершин от начального и конечного положения производящего куба). Подсчитаем число ребер. У единичного отрезка AB есть лишь одно ребро (сам отрезок AB). У единичного квадрата ABCD — четыре стороны, («ребра»), у единичного куба ABCDEFGH — двенадцать ребер (по четыре ребра от начального и конечного положений производящего квадрата и четыре ребра, описанных четырьмя вершинами производящего квадрата), а у четырехмерного единичного куба тридцать два ребра (по двенадцать ребер от начального и конечного положений производящего куба и восемь ребер, описанных восемью вершинами производящего куба). Подсчитаем теперь число граней. У единичного квадрата ABCD есть лишь одна грань (сам квадрат ABCD). У единичного куба ABCDEFGH имеется шесть граней (по одной грани от начального и конечного положения квадрата ABCD и четыре грани, описанные сторонами производящего квадрата), а у четырехмерного единичного куба имеются двадцать четыре грани (по шесть граней от начального и конечного положений производящего куба и двенадцать граней, описанных ребрами производящего куба). Подсчитаем наконец число граничных кубов. У куба ABCDEFGH есть лишь один граничный куб (сам куб ABCDEFGH), а у четырехмерного единичного куба имеется восемь граничных кубов (по одному кубу от начального и конечного положения производящего куба и шесть кубов, описанных гранями производящего куба).

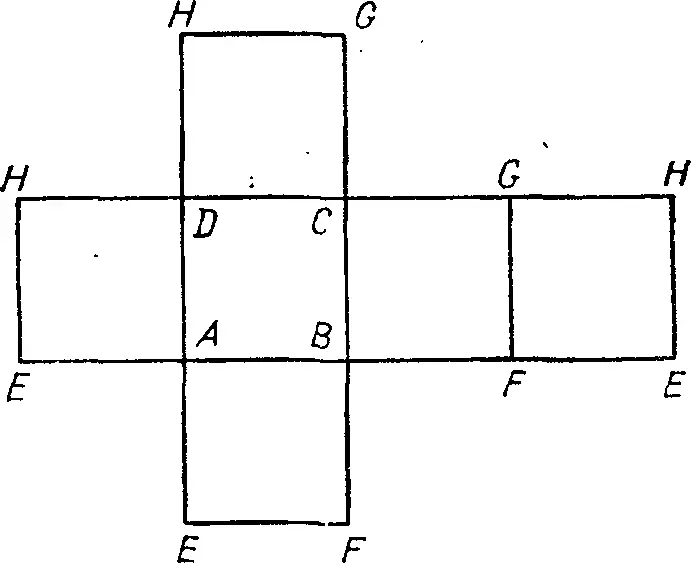
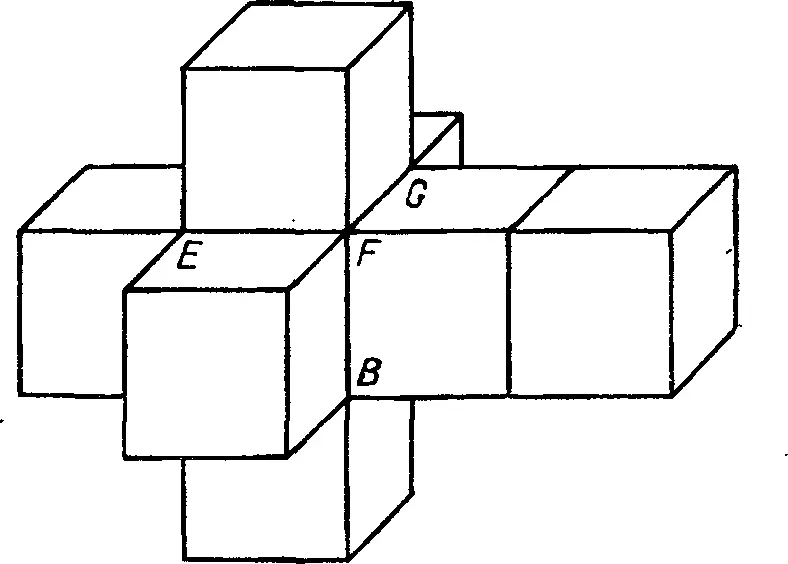
Предположим, что граница квадрата ABCD сделана из проволоки. Перерезав проволоку в вершине D, мы сможем развернуть границу квадрата и совместить ее с прямой, на которой лежит отрезок AB. При этом у нас получится одномерная фигура (рис. 2) длиной в четыре единицы. По обе стороны исходного единичного отрезка AB располагаются единичные отрезки DA и BC. Кроме того, к отрезку BС примыкает еще один единичный отрезок CD . Предположим теперь, что грани куба ABCDEFGH сделаны из тонкой фольги. Разрезав фольгу вдоль ребер EF, GH, HE, AE, BF, CG и DH , мы сможем развернуть поверхность куба на плоскость и получим двумерную фигуру, составленную из шести квадратов. К квадрату ABCD с каждой стороны примыкают единичные квадраты. Кроме того, к одному из таких квадратов примыкает еще один единичный квадрат FEGH (рис. 3). Аналогично если предположить, что кубы, ограничивающие четырехмерный единичный куб, сделаны из дерева и мы провели распилы вдоль соответствующих граней, то граничные кубы можно будет развернуть в трехмерную фигуру, составленную из восьми единичных кубов. К каждой грани куба ABCDEFGH примыкает по одному кубу. Кроме того, к свободной грани одного из примыкающих кубов «приклеен» еще один куб (рис. 4). Восемь кубов, образующих трехмерную фигуру, изображенную на рис. 4, составляют границу четырехмерного куба.
Ниже перечислены элементы, составляющие единичный отрезок, квадрат, куб и четырехмерный куб, а также их границы.
| Число точек | Число отрезков прямых | Число квадратов | Число кубов | |
| Одномерный отрезок | M | 1 | 0 | 0 |
| Двумерный квадрат | M ² | M | 1 | 0 |
| Трехмерный куб | M ³ | M ² | M | 1 |
| Четырехмерный куб | M ⁴ | M ³ | M ² | M |
| Число вершин | Число ребер | Число граней (квадратов) | Число трехмерных граней (кубов) | |
| Граница одномерного отрезка | 2 | 1 | 0 | 0 |
| Граница двумерного квадрата | 4 | 4 | 1 | 0 |
| Граница трехмерного куба | 8 | 12 | 6 | 1 |
| Граница четырехмерного куба | 16 | 32 | 24 | 8 |
Приведенные выше рассуждения допускают непосредственное обобщение па случай единичного куба и более высоких размерностей.
Читать дальшеИнтервал:
Закладка:










