Грег Иган - Заводная ракета

Ялда изучила диаграмму.

— То есть ты движешься вдоль горизонтальных линий энергии до точки пересечения с графиком, а затем опускаешь перпендикуляр на ось импульса?

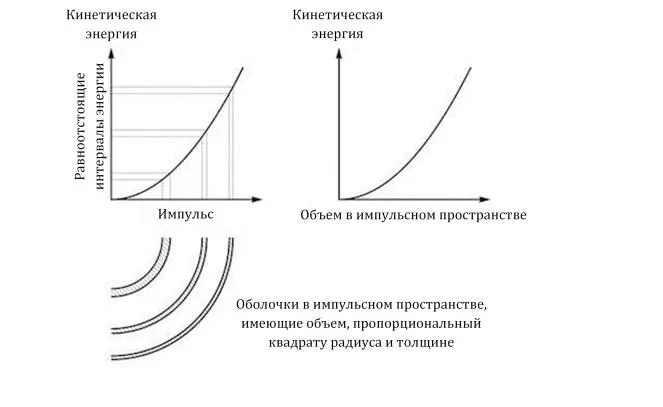
— Верно, — подтвердил Корнелио. — Но не забывай, что импульс — это векторная величина. Энергия определяет разброс длин этого вектора, но не дает никакой информации о его направлении. Частица может двигаться на север, на запад, вверх, вниз; этого мы не знаем. Так вот, мы берем стрелку известной длины и начинаем размахивать ею относительно начальной точки, во всех возможных направлениях. В этом случае конец стрелки описывает сферу — а точнее, сферическую оболочку, так как длина стрелки может меняться в определенных пределах. Объем этой оболочки в «импульсном пространстве» определяет весь спектр возможностей, доступных нашей частице при условии, что ее энергия находится в заданном интервале.

— Значит, ты нарисовал фрагменты этих оболочек, построил график зависимости между их объемом и кинетической энергией…, и оказалось, что этот график выглядит точно так же, как и в случае самого импульса.

— Это верно для данного примера, — сказал Корнелио, — но не в общем случае! Так что забудь об их сходстве и сосредоточься на правом графике. О чем он тебе говорит?

— Объем в импульсном пространстве возрастает с увеличением кинетической энергии, — сказала Ялда. — Это вполне логично. Импульс более быстрой частицы соответствует сфере большего размера; с ростом импульса оболочки становятся тоньше, но это с лихвой компенсируется увеличением площади их поверхности.

— Иначе говоря, объем увеличивается, — согласился Корнелио. — Но в какой момент скорость его роста максимальна?

— В самом начале, — ответила Ялда. — Когда энергия мала, объем стремительно нарастает; в дальнейшем его рост замедляется.

— Именно.

— Но что из этого следует?

— Частицы сталкиваются друг с другом, отскакивают, обмениваются энергией. — объяснил Корнелио. — Дай частице чуть больше энергии, когда ее первоначальная энергия мала , и объем в импульсном пространстве резко увеличится. А если источником дополнительной энергии служит столкновение с другой, более быстрой частицей, то объем, соответствующий этой более быстрой частице, уменьшится — но не на ту же самую величину .

— Значит… нужно сложить два объема? — предположила Ялда. — А потом посмотреть, как эта сумма меняется при переносе энергии между двумя частицами?

— Не совсем, — сказал Корнелио. — Объемы перемножаются . Каждый объем определяет количество возможностей, которыми располагает конкретная частица — а каждую из возможностей, имеющихся в распоряжении первой частиц, можно скомбинировать с любой из возможностей второй. Отсюда и берется произведение объемов. — Он нарисовал новую диаграмму.

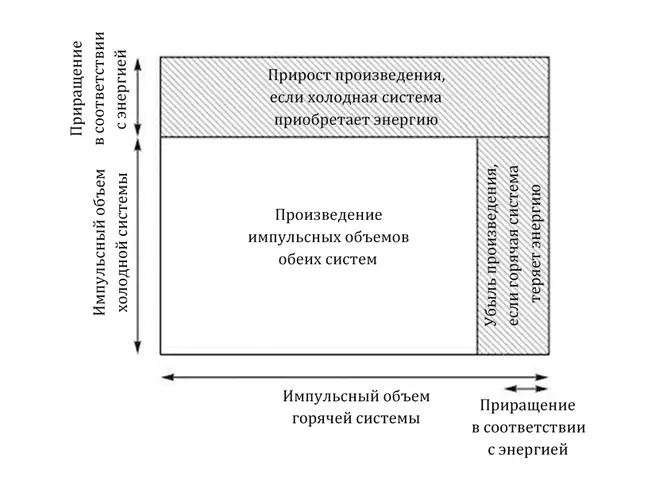
— Если энергия передается от одной системы к другой, то произведение их объемов в импульсном пространстве возрастает вдоль одной из сторон прямоугольника и убывает вдоль другой. И от того, какое из этих изменений больше, зависит общий прирост этого произведения.

— Ты называешь одну из систем «горячей», а другую — «холодной», но откуда во всех этих рассуждениях берется температура? — спросила Ялда.

— Каждой системе можно сопоставить отношение ее объема в импульсном пространстве к скорости его роста относительно энергии. — сказал Корнелио. — Тем самым ты закодируешь в одном числе всю необходимую информацию — это и есть температура. Когда одна из систем имеет более высокую температуру — при условии, что температуры обеих систем одновременно положительны или отрицательны — отсюда сразу следует вывод: если первая система будет отдавать энергию в пользу второй, то общий диапазон возможностей увеличится. Именно поэтому энергия и перемещается от горячих тел к холодным — у результирующей системы число возможностей больше.

— Фух. — Ялда изобразила у себя на груди копию диаграммы Корнелио и выполнила заключительную стадию расчетов. — Получается, что в нашем простейшем примере температура… пропорциональна кинетической энергии! Столько трудов, и все ради того, чтобы вернуться к наивному представлению об их равнозначности.

Корнелио удержался от дальнейших замечаний в ее адрес.

— Разумеется, настоящее определение не противоречит всему, что ты знаешь — в случае идеального газа, с точки зрения старой физики. Но если ты по-прежнему цепляешься за идею эквивалентности температуры и энергии, то посмотри, какие выводы мы сделали, исходя из твоей собственной работы.

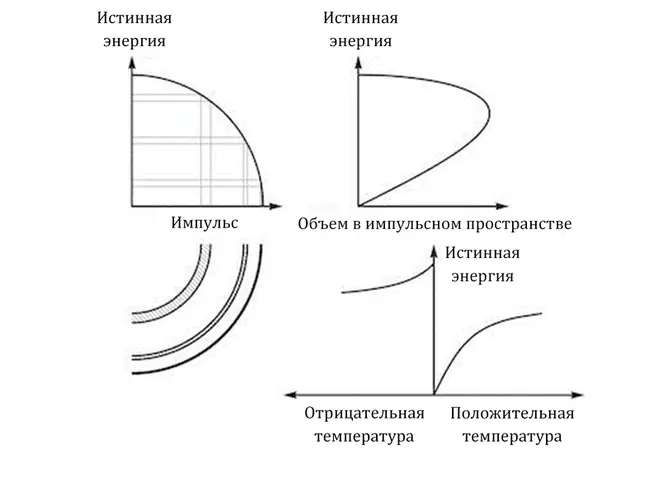
Ялда пристально посмотрела на его кожу, покрытую тонкими выпуклыми линиями, и ощутила справедливый стыд. Поначалу ей казалось, что ее просто дурачат, но когда она попыталась воспроизвести шаги, которые он описал для простейшего случая, во всей этой странной конструкции появилась какая-то пугающая неизбежность.

Истинная энергия и импульс были связаны посредством окружности, и переходили друг в друга в результате поворота осей. По мере того, как импульс частицы возрастал от нуля, ее истинная энергия начинала падать, и поначалу поведение частицы почти не отличалось от более ранних расчетов — разве что график был нарисован вверх ногами.

Однако импульс частицы не может безгранично возрастать по мере ее ускорения. С приближением импульса к своему максимальному значению оболочки в импульсном пространстве не только замедляли свой рост, но еще и становились тоньше. На отметке около 2/3 максимальной энергии оболочки достигали наибольшего объема — после этого их объем начинал снижаться.

В этот момент зависимость между количеством возможностей, доступных этой частице, и изменением энергии менялась на противоположную. Медленная частица могла расширить свои возможности за счет небольшого ускорения… в то время как частица, обладающая достаточно большой скоростью, от дальнейшего разгона свои возможности, наоборот, теряла. Из-за ограниченной величины импульса наверху становилось тесно.

Точно такой же закономерности подчинялась и температура, которая меняла знак при достижении пикового объема сферической оболочки. И несмотря на то, что отрицательные температуры сами по себе могли быть результатом какого-то специфического выбора единиц измерения, диаграмма Корнелио ясно давала понять, что и положительные, и отрицательные температуры были вполне реальным явлением. Их наименования всегда можно было поменять местами, подправив соответствующие определения, однако грань, отделяющую минус от плюса, устранить было нельзя.