Александр Казанцев - Собрание сочинений в трех томах. Том 2. Клокочущая пустота.

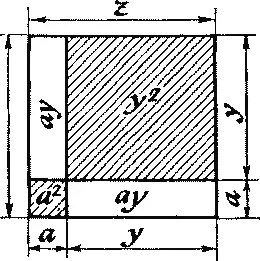
Если, как следует из квадрата орнамента, z = y + a , то z 2= x 2+ y 2 будет иметь вид z 2= y 2+ (a 2+ 2ay) и x 2= a(a + 2y) . Если a = α 2 и ( a + 2 y ) = β 2то x = αβ, y = ( α 2— β 2)/2; z = ( α 2+ β 2)/2.

Из выражения для « y », где в числителе разность квадратов α и β, ясно, что хотя бы одна из этих величин не может быть четной, иначе « y » не будет целым числом. Случай с иррациональными числами рассмотрен в последующем примечании.

Для возрастающих коэффициентов α и β можно составить таблицу, из которой вытекает ряд закономерностей, в частности формулировка новой теоремы. Нечетный катет простейших пифагоровых троек в целых числах разлагается на два взаимно простых сомножителя, квадраты которых соответственно равны сумме или разности гипотенузы и второго катета , то есть в дополнение к теореме Пифагора: α 2= z — y; β 2= z + y .

x = m 2— n 2; y = 2mn; z = m 2+ n 2. (Примеч. авт.)

Примечание автора для особо интересующихся . Если положить α = m + n; β = m — n, то x = αβ = (m + n)(m — n) = m 2— n 2; y = 2mn; z = m 2+ n 2 , что и было записано Декартом.

Примечание автора для особо интересующихся. Вертикальные ряды x представляют собой арифметические прогрессии с показателем = 2 β . Все значения сторон треугольников с возрастанием ряда изменяются по арифметической прогрессии, показатель которой для y — постоянен и равен 4, а для x и z увеличивается с порядковым номером ряда и порядкового номера тройки в вертикальном ряду и равен 4 ( β + i — 1), где i — порядковый номер тройки в ряду.

Примечание автора для особо интересующихся. Если α = p√2e, β = q√2e , то p и q могут быть и четными и нечетными, x = αβ = 2 pqe, y = ( p 2— q 2) e; z = ( p 2+ q 2) e , то есть p и q тождественны m и n древних формул (см. пред. примеч.), x и y просто меняются местами, к тому же, помноженные на e , не являются простейшими.

Примечание автора для особо интересующихся. Золотое сечение было известно древним зодчим, но сформулировано Леонардо да Винчи. Цифры 3, 5, 8, 13 совпадают с частью ряда Фибаначчи, помогающего современным ученым объяснять ряд явлений природы (1, 1, 2, [3, 5, 8, 13,]21, 34 и т. д.).

Примечание автора для особо интересующихся. По теории Эйнштейна, масса тела m , летящего со скоростью v при массе покоя m 0и скорости света c , меняются по формуле

Это выражение легко преобразуется в m 2= m 0 2— (( v / c ) m ) 2или графически в Δ.

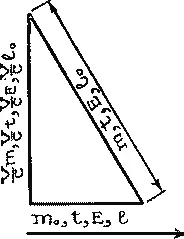
Тот же закон прямоугольного треугольника отражен и в сокращении длины покоящегося тела l 0до l в полете, и парадоксе времени теории относительности (преобразования Лоренца) при t 0— прошедшее время неподвижного наблюдателя, t — время на улетевшем от него объекте и c — скорость света:

или l 2= l 0 2— (( v / c ) l 0) 2— опять Δ,

t 0= t √(1 — ( v / c ) 2), откуда t 0 2= t 2— (( v / c ) t ) 2; Δ узнаем закон Пифагора.

И наконец, тот же закон скажется и на энергии летящего тела E при энергии его покоя E 0; E 2= E 0 2+ ( v / c ) E 2; — Δ. Таким образом, все парадоксальные эффекты теории относительности подчинены основному закону Пифагора.

Лет двадцать назад во времена египетского президента Насера, стремившегося к дружбе своего народа с СССР, в Каире и Александрии гастролировал наш Большой театр, и друг автора, артист балета С. А. Салов, приобрел на рынке фотографию обугленного музейного документа, который, как ему казалось, может заинтересовать фантаста. По сохранившейся части таблицы автору удалось благодаря ранней работе заслуженного деятеля науки и техники РСФСР профессора М. М. Протодьяконова ее восстановить. (Примеч. авт.)

Впоследствии она получила название Тридцатилетней. (Примеч. авт.)

Трудный юридический случай. (Примеч. авт.)

Свои выводы по теории вероятностей Ферма опубликовал лишь по инициативе Паскаля в 1654 году, а применение этой теории в судебном деле нашло своих теоретиков лишь спустя более чем столетие в трудах маркиза Кондерса, а также Лапласа и Пуассона. (Примеч. авт.)

Омнибус, предложенный Б. Паскалем. (Примеч. авт.)

Примечание автора для особо интересующихся. Метод Ферма, в свое время несправедливо оспоренный Декартом, предвосхищал дифференциальное и интегральное исчисление, хотя задачу решал алгебраически, без анализа бесконечно малых величин. В задаче разбивки прямой с длиной « a » на две части, так, чтобы квадрат одной ( x 2), помноженный на величину другой части = ( a — x ), был бы максимальным, он приравнивал 2 ax — 3 x 2к нулю и получал, что x = 2/ 3 a , то есть заменял современное дифференцирование и взятие первой производной.

Правота Торричелли была подтверждена знаменитым опытом Герике, получившим название «Магдебургские полушария», проведенным в Магдебурге лишь в 1654 году и доказавшим существование атмосферного давления. Торричелли принадлежит изобретение ртутного барометра и создание над ртутным столбом «торричеллиевой пустоты». (Примеч. авт.)

Примечание автора для особо интересующихся . Автору удалось восстановить позицию

См. левую диаграмму. Последовало: 1. Л: g1! ( 1. e7? fg 2. e8Ф Кf8+ 3. Крd8 Л: e8+ 4. Кр: e8 с шансами у черных) Л: g1 2. Сe5+! de 3. e7 Л: g5 4. Кd5 Кf6 5. К: f6 Кр: f6 6. e8К мат!

См. правую диаграмму. 6. e8Ф? f4 7. Фe7 + Крf5 8. Ф: f7 + Крg4 9. Фe6 + Лf5! 10. Ф: g6 + Л: g5 11. Фe6 + Лf5 12. Фg8 + Лg5, в лучшем случае для белых — ничья.

Эта мысль была высказана британским генералом на три с четвертью столетия раньше, чем в наше время (когда она звучит уже угрозой самому существованию человечества) американским генералом Александром Хейгом в бытность его государственным секретарем в администрации президента Р. Рейгана. (Примеч. авт.)