Роберт Хайнлайн - Рассказы. Миры Роберта Хайнлайна. Том 25

2) Пользуйтесь одинаковыми единицами измерения. Если начали с сантиметров, считайте и далее в сантиметрах, если в милях, то и далее в милях. Четверть пути равна 30 миллионам миль, или 4.827 X 10 в 12-й степени сантиметрам.

И последнее: поскольку нам нужно именно время полета, преобразуем последнее уравнение таким образом, чтобы вы получили ответ на калькуляторе за одну операцию. Я уже сделал так много упрощений и отбросил столько мелких переменных, что буду рад получить ответ с точностью до двух значащих цифр.

Итак, если d/(0.5a)=1 в квадрате, то t равно квадратному корню из d/(0.5a).

Вводим в калькулятор расстояние (d) 30 миллионов миль, делим на половину от 0.1g. Нажимаем кнопку квадратного корня. Умножаем на четыре. Мы получили время пути, выраженное в секундах, поэтому делим его на 3600, получаем в часах, делим еще на 24 и получаем в днях.

Тут вам полагается удивиться и начатать искать ошибку. Пока вы этим занимаетесь, схожу возьму пива из холодильника.

Ошибки нет. Пересчитайте снова, на этот раз в метрической системе. Найдите справочник и проверьте уравнения. Ответ вы найдете чуть ниже, но пока в него не заглядывайте; мы поговорим о других путешествиях, которые вы сможете совершить в 2000 году, если говорите дома на японском или немецком — или даже английском, если Проксмайр и его присные не будут переизбраны.

Подсчитайте длительность того же пути, но только при ускорении в одну сотую g. При такой тяге я буду весить меньше собственных ботинок.

Гм-м! Получается, что один из ответов ошибочный.

Потерпите немного и на этот раз повторите вычисления для ускорения в одно g — того самого, что вы испытываете, лежа в кровати. (См. статью Эйнштейна, написанную в 1905 году)

(Странно. Должно быть, все три ответа ошибочны.)

Потерпите еще немного. Давайте решим все три задачки снова, но для полета к Плутону — в 2006 году плюс или минус год. Почему именно в этом? Потому что сейчас Плутон нырнул внутрь орбиты Нептуна и не достигнет перигелия до 1989 года, а я хочу, чтобы он находился подальше — у меня в шляпе припасен кролик.

Плутон вынырнет обратно в 2003 году и в 2006 году будет (с точностью до пары миллионов миль) на расстоянии в 31.6 астрономических единиц (АЕ) от Солнца. Одна АЕ равна 92.9 миллиона миль, или 1.496 X 10 в 13-й степени сантиметрам.

Теперь посчитайте длительность полета туда и обратно (63.2 АЕ) с постоянным ускорением в одну, одну десятую и одну сотую силы тяжести. Свои труды мы посвятим Клайду Томбо — единственному живущему среди нас человеку, открывшему новую планету и затратившему на это месяцы кропотливого труда по изучению тысяч астрономических фотографий.

Некоторые полагают, что Плутон некогда был спутником другой планеты, и его малые размеры делают это предположение вероятным. Но сейчас это не спутник. Он и слишком велик, и слишком далек от Солнца, чтобы быть астероидом или кометой. Так что это планета — или нечто настолько экзотичное, что представляет собой еще более ценную добычу.

Плутон остается самым таинственным и самым интригующим небесным телом. Планета размером и массой с Марс, но очень далекая может и не представлять особого интереса… но представьте ее в роли заправочной станции. Во многих художественных произведениях и научных проектах говорится об использовании газовых гигантов и/или колец Сатурна как источников горючего. Но если Плутон состоит из метанового или водяного льда, замерзшего водорода или их смеси, те как источник горючего — обычного, ядерного иди просто реакционной массы — Плутон имеет одно чрезвычайно важное преимущество перед газовыми гигантами: он не находится на дне ужасающе глубокого гравитационного колодца.

Кончили считать? Тогда посмотрите на таблицу.

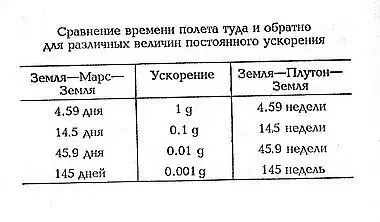
Вот вам и кролик из шляпы. Вы уже заметили, что цифры длительности пути в обеих колонках совершенно одинаковы, только для Марса они означают дни, а для Плутона — недели, то есть для кораблей любой конструкции, но с постоянным ускорением Плутон всего в семь раз дальше, чем Марс, хотя расстояние-до Плутона в милях примерно в 50 раз больше.

Я добавил еще пример для величины ускорения в одну тысячную силы тяжести, потому что сейчас (я пишу это в 1979 году) мы не знаем, как построить КПУ для долгих полетов при 1 g, 0.1 g и даже 0.01 g; третий закон Ньютона (из которого можно вывести все остальные законы реактивного движения) пока подрезает нам крылья. Но только временно. Есть еще и Е=m*c_в_квадрате, есть и несколько способов «питаться подножным кормом», набирая прямо в космосе необходимую реакционную массу. Наберитесь терпения, все это еще очень ново. Большинство из вас, читающих эти строки, доживет до появления кораблей, способных выдавать постоянно 0.1 g или даже больше, — и вы еще сможете провести отпуск в космосе — и скоро! Я, вероятно, до них не доживу, но вы сможете. (Я не жалуюсь, сержант, — я родился в век лошади с телегой, а дожил до того дня, когда увидел шагающих по Луне людей и прямую трансляцию с поверхности Марса. Я свою долю получил!)

Но если вас устраивает постоянное ускорение порядка 0.001 g, мы можем начать космический проект хоть сегодня, потому что уже имеется несколько способов постройки кораблей с таким ускорением — хотя бы со световым парусом.

Я предпочитаю говорить именно о таких, летящих под дуновением «солнечного ветра», потому что последний добавленный мною пример (0.001 g) показывает, что вся Солнечная система доступна нам прямо сейчас и нет никакой необходимости дожидаться 2000 года и разных технологических прорывов.

Десять недель до Марса… полет до Плутона и обратно на расстояние 31.6 АЕ за 2 года и 9 месяцев… или такой же полет до афелия Плутона, самой дальней известной нам точки системы (более удаленной, чем зимний дом комет).

Десять недель… пилигримам на «Мэйфлауэре» потребовалось девять недель и три дня, чтобы пересечь Атлантику.

Два года и девять месяцев — такой была в прошлом веке нормальная длительность коммерческого плавания для клипера, направляющегося из Бостона в Китай… а ведь купцы-янки после таких плаваний богатели.

Три года и двадцать пять недель — многовато для торговли с Китаем в XIX столетии… но никто и не захочет отправляться в столь длительный полет к Плутону, потому что Плутон достигнет афелия лишь в 2113 году, а к тому времени у нас будут корабли, которые смогут долететь до него (с постоянным ускорением и разворотом на середине пути) за три недели.

Прошу вас также отметить, что Англия, Голландия, Испания и Португалия создали империи планетного масштаба при помощи кораблей, у которых на дорогу туда и обратно уходило столько же времени, сколько уйдет у космического корабля с ускорением в 0.001 g. В открытом море или космосе важно не расстояние, а время. Все впечатляющие достижения наших астронавтов были достигнуты во время инерционных полетов, в невесомости, и потому могут быть приравнены к плаванию на плоту по Миссисипи. Но даже самое малое постоянное ускорение превращает Солнечную систему в прибыльное коммерческое предприятие.