Александр Казанцев - Клокочущая пустота (с иллюстрациями)

— Это действительно увлекает.

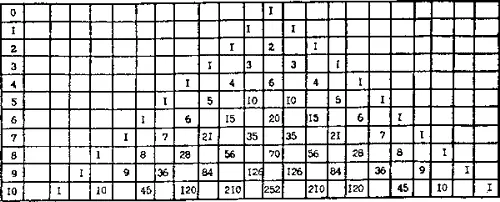
— Что ты! Это пустяк по сравнению с истинной вершиной красоты. Зачем все эти сложные математические зависимости, если все определяет единственная, но всеобъемлющая? Всмотрись внимательнее в таблицу и, пожалуйста, не разочаровывай меня. Ищи!

Самуэль с интересом вглядывался в письмо Паскаля.

— Отец! Это непостижимо, я просто случайно наткнулся на удивительное свойство! Ведь каждое число в таблице равно сумме двух, расположенных над ним в предыдущем горизонтальном ряду!

— Браво, мой мальчик! Ты будешь ученым! Если искать подлинную математическую красоту, то вот она! Удивительное свидетельство существования таких математических тайн, о которых мы и не подозреваем. [35] В своем 42-м замечании на полях книги «Арифметика» Диофанта Пьер Ферма записал по-латыни: «…наука о целых числах, которая, без сомнения, является прекраснейшей и наиболее изящной, не была до сих пор известна ни Боше, ни кому-либо другому, чьи труды дошли до меня (Боше де Мазариак — математик, издавший в переводе на латынь с древнегреческого «Арифметику» Диофанта, снабдив ее своими комментариями и дополнениями, ставшую настольной книгой Ферма). (Примеч. авт.)

— Да, отец, я понимаю тебя. Есть от чего прийти в восторг! Мне это представляется пределом достижимого.

— Как ты сказал? — сощурился Пьер Ферма. — Пределом достижимого? Пусть никогда эта повязка не закрывает твоих глаз ученого. Никогда воображаемый или даже увиденный «предел достижимого» не должен останавливать тебя в будущем как ученого.

— Я понимаю тебя, отец, и не понимаю.

— Я признаюсь тебе, Самуэль. Красота математической зависимости в таблице — это лишь сочетание граней частных случаев. А подлинная, всеобъемлющая красота — в обобщении. Ты понял меня?

— В обобщении? Ты хочешь сказать, что можно представить бином в какой-то степени в общем виде?

— Именно эту задачу я и поставил перед собой.

— Ты восхищаешь и поражаешь меня, отец. Придя в такой восторг от открытия Паскаля, ты пытаешься уйти вперед, возвыситься над таблицей частных значений!

— То, что может быть вычислено, должно и может быть представлено в виде универсальной формулы.

— Неужели ты нашел ее, отец?

— Да. Я еще никому не показывал ее, но подготовил письмо Каркави, заменившему почившего беднягу аббата Мерсенна, чтобы тот разослал копии европейским ученым. Журнала у нас все еще нет.

— Но, отец, не требуй от близких больше того, что они способны дать.

— Ты учишь меня разумному. Я всю жизнь стараюсь руководствоваться этим принципом.

— Так покажи мне формулу и вывод ее.

— Ты хочешь, чтобы я нарушил свой принцип? Нет, друг мой и сын мой! Даже для тебя я не сделаю исключения. Хочешь видеть мой БИНОМ — пожалуйста. Но получить его с помощью математических преобразований попробуй сам. Я хочу убедиться, что ты станешь подлинным ученым.

— Но я не решусь соперничать с тобой.

— Это не соперничество. Труднее всего достигнуть конечной цели, не зная ее, а если она известна, то дорогу к ней найти легче.

— Но ко многим указанным тобой целям ученые так и не могут найти дороги. Потому так и ждут твоего собрания сочинений.

— Ты опять об этом. Лучше я тебе покажу свою формулу: (x + y) n= (Mx + y) n+ (x + My) n! — Он написал ее тростью сына на песке.

— Но как же мне найти дорогу к этой вершине?

— Я чуть-чуть помогу тебе, из отцовских чувств, конечно! Видишь ли, когда-то я предложил систему координат, которой воспользовался, в частности, мой друг Рене Декарт.

— Ему нужно было бы при этом больше сослаться на тебя.

— Я предложил систему координат, чтобы ею могли пользоваться все математики, которые найдут ее удобной, и не требую от них специальных поклонов в мою сторону.

— Ты остаешься самим собой, отец! Право, хотелось бы позаимствовать у тебя такие примечательные черты характера, которые поднимают тебя и надо мной, и над всеми. Итак, система координат?

— Теперь я пошел дальше. Ведь никогда не надо останавливаться на достигнутом. Я решил воспользоваться сразу двумя системами координат — прямой и перевернутой. Это позволило мне создать метод совмещенных парабол.

— Очень интересно! Но как это понять?

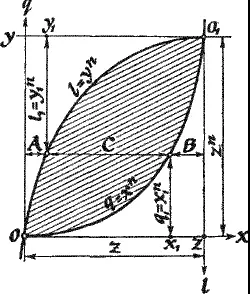
И Пьер Ферма стал объяснять сыну суть своего метода, снова взяв у него трость, чтобы чертить на песке. [36] Примечание автора для особо интересующихся. Метод совмещенных парабол Пьера Ферма сводится к тому, что в системе прямоугольных координат (декартовых!) с горизонтальной осью x и вертикальной q — (xO 1 q) — вычерчивается парабола по уравнению q = x n . Чертеж поворачивается на 180°, и на нем наносится (см. рис.) еще одна система прямоугольных координат (yO 1 l) с горизонтальной осью «у» и вертикальной «l». Вертикальные оси двух систем координат отстоят одна от другой на величину z, а горизонтальные на z n . В перевернутой системе координат тоже вычерчивается точно такая же парабола по уравнению l = y n . Две совмещенные таким способом параболы образуют полусимметричную геометрическую фигуру, ограниченную ими. Выбирая точку x 1 на оси x, строим от нее вертикальный отрезок (до пересечения с первой построенной параболой) с длиной g 1 = x 1 n . Проведя теперь горизонтальную линию от пересечения вертикального отрезка с параболой через фигуру до второй параболы, получим точку, вертикальный отрезок от которой до оси у перевернутой координатной системы отметим на оси y точку y 1 . Длина же этого отрезка, равная ординате перевернутой параболы, будет l = y n . Из построения следует: q + l 1 = x 1 n + y 1 n = z 1 n . Диофантово уравнение, положенное Ферма в основу его Великой теоремы. Все это восстановлено А. Н. Кожевниковым.

Ферма закончил формулой x n+ y n= z nи вернул сыну трость.

— Но ведь это же Диофантово уравнение! — воскликнул Самуэль.

— Ты прав. Мне еще придется заняться им. Примечательно, что оно получается из геометрического построения. Этим же построением можешь воспользоваться и ты, если не раздумал еще доказать формулу моего «бинома».

— Я попробую, отец, но ты, вероятно, переоцениваешь мои силы.

— Напротив, я надеюсь на тебя! Передаю тебе факел, как написал в своем письме.

— Сестричка! — воскликнул Самуэль.

На аллее показалась Сюзанна, худая и прямая, с холодным красивым лицом, так гордо несущая голову, что взгляд ее серых глаз казался едва ли не надменным.

— Мама просит к столу. Обед подан, — пригласила она.

Отец и сын поднялись и зашагали следом за девушкой, невольно любуясь ее осанкой. Она только раз обернулась, чтобы бросить на брата оценивающий взгляд. Тот, сняв шляпу, шутливо раскланялся.