Ричард Маккенна - «Если», 1994 № 10

— Что означает эта линия? Она проходит спереди или сзади? Я правильно понял?

Мэри отвечала то смешком, то «нет-нет» (тут проблем с порядком слов не возникало) и принималась чертить. Я брал готовые листы, пропускал через ксерокс, вынимал и позволял ей водить по чертежам моей ладонью. Но дело продвигалось туго; издав раздраженный возглас, Мэри вернулась к моделям, начала соединять между собой треугольники, составлять прямые. Впрочем, здесь мы тоже далеко не ушли.

— Нужно чертить, — сказала она.

— Понятно. Тогда пишите и читайте.

Мы продолжали работать: она писала и либо читала, либо передавала страницы мне, а я пропускал их через ксерокс в режиме «перевод в шрифт Брайля». Джереми, судя по всему, внимательно наблюдал за происходящим.

Постепенно мы подобрались очень близко к сути моих исследований. (Холодное прикосновение.) Предположив, что субатомные частицы совершают свои «прыжки» в микроизмерениях, я разработал n-мерную топологическую систему, где n больше единицы и меньше бесконечности, поэтому изучаемый континуум находится в промежутке между единицей и некоторым конечным числом измерений, переходя из кривой в нечто, если хотите, вроде швейцарского сыра, в зависимости от количества энергии, проявляемой в пространстве в любой из четырех форм — электромагнетизме, гравитации, а также в форме сильных и слабых взаимодействий. Геометрия этой системы, столь схожей с опытным, тактильным пространством, привлекла, как я уже сказал, внимание физиков, однако исследования еще не были доведены до конца, и я не публиковал даже промежуточных результатов.

И вот я сижу в своем кабинете и «общаюсь» с молодой женщиной, которая в обычном разговоре не может правильно построить фразу, однако на математическом языке изъясняется вполне понятно и рассуждает, интересуется моей мало кому известной работой.

Той, о которой меня столь часто и с большим любопытством расспрашивал Джереми Блесингейм.

Я вздохнул и откинулся на подушки. Наша беседа. растянулась на два или три часа. Мэри пожала мою руку. Я не знал, что думать.

— Я устал.

— А мне лучше, — откликнулась она. — Так разговаривать проще.

— Да? — Я взял в руки модель позитрона, врезающегося в «стационарный» мюон: проволочное дерево, ствол которого неожиданно превращается в густую крону… Ряд событий, невообразимое количество объяснений… Впрочем, большинство частиц летело в одном направлении (словно истины осязательного пространства).

Мэри отпустила свою ладонь и взялась рисовать последний чертеж, с которого потом сделала ксерокс, после чего приставила мои пальцы к выпуклым линиям.

Снова теорема Дезарга: треугольники АВС и А'В'С», проецируемые из точки О. Правда, на сей раз оба треугольника находились в одной плоскости, прямые АВ и А'В' были параллельны, как. ВС и В'С', АС и А'С'. Точки Р, О и К превратились в идеальные. Мэри вновь и вновь ставила мои пальцы в те места, где располагались эти точки.

С. Пожалуй, следует объяснить поподробнее, ибо теперь мы оставляем позади мир евклидовой геометрии.

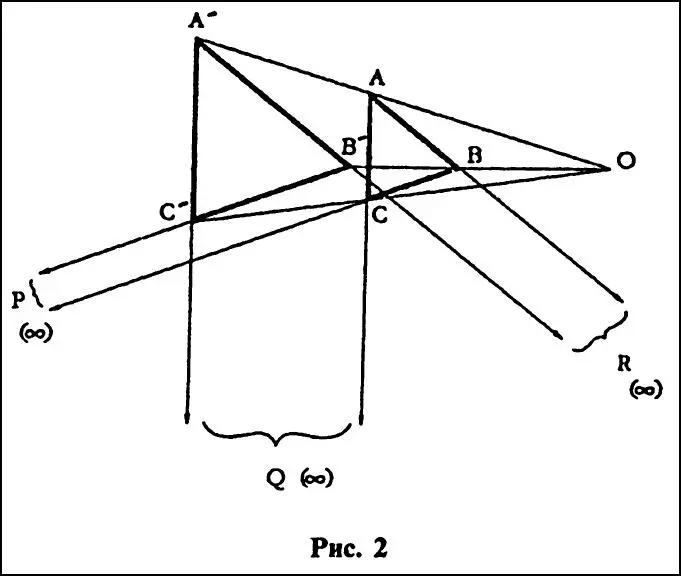
Геометрия обычных точек и прямых (евклидова) значительно осложняется тем фактом, что две параллельные прямые не встречаются ни в одной точке. Почему? Изменение пятой теоремы Евклида относительно параллельных прямых привело к появлению первых неевклидовых геометрий Лобачевского, Больяи и Римана. Чтобы войти в изменившийся мир, необходимо всего лишь прибавить к обычным точкам каждой прямой по одной «идеальной». Эта точка принадлежит всем прямым, параллельным данной. Отныне каждая пара прямых на плоскости будет пересекаться в одной точке: непараллельные в обычной, а параллельные — в идеальной, общей для двух прямых. Кто-то догадался назвать такую точку «точкой в бесконечности».

Понятие идеальности можно распространить и на другие геометрические фигуры: все точки в бесконечности на одной плоскости лежат на прямой в бесконечности; все прямые в бесконечности находятся на плоскости в бесконечности; идеальная плоскость располагается в пространстве, за пределами остальных, а все идеальные плоскости — в пространстве в бесконечности, в следующем измерении. И так далее, до энного измерения. В осязательном пространстве невскианской геометрии я ощущаю присутствие этих идеальных миров, ибо за отдельными идеальными плоскостями-мембранами, что вне моей досягаемости, существуют идеальные действия, которые я могу только воображать, только желать…

Заметьте, кстати, что, прибегая к понятию идеальной точки, мы можем доказать теорему Дезарга для одной плоскости. Помните: чтобы доказать любую теорему, достаточно доказать частный случай, как здесь, где АВ параллельно А'В', ВС параллельно В'С', а АС — А'С'. Поскольку пары прямых параллельны, они пересекаются в своих идеальных точках, которые, чтобы было удобнее, назовем Р, О и К. А поскольку все идеальные точки плоскости лежат на прямой в бесконечности, значит, Р,'O, и К коллинеарны. Все просто. Таким образом доказывается не только частный случай, когда стороны треугольников параллельны, но и все прочие, когда параллельности не наблюдается.

Если бы мир соответствовал этой неоспоримой логике!

А'АО. Тут Мэри сказала:

— Мистер Блесингейм, принесите, пожалуйста, воды.

Джереми послушно вышел из кабинета. Мэри быстро зажала мой указательный палец между своими средним и большим (настолько сильно, что подушечки словно расплющились, а мне стало больно), дважды надавила, затем ткнула сначала, в собственную ногу, а затем в чертеж и провела пальцем по одной из сторон треугольника. Повторив все еще раз, она приставила мой палец к моей же ноге, после чего приложила его к стороне другого треугольника. Понятно, мы с ней параллельны, нас проецируют из точки О, которая…

Правда, у точки О Мэри раз за разом останавливалась. Что она хочет сказать?

Вернулся Джереми. Мэри отпустила мою руку. Какое-то время спустя мы распрощались — крепкое рукопожатие, дрожащая ладонь, — и они ушли..

— Джереми, — спросил я, когда он возвратился, — могу ли я поговорить с ней наедине? Мне кажется, в вашем присутствии она нервничает. Должно быть, малоприятные ассоциации. Я столкнулся с действительно любопытным подходом к проблеме n-мерной системы, однако вы отвлекаете Мэри, и она теряет нить мыслей. Я хотел бы пригласить ее на прогулку — вдоль канала, или к Тайдл-Бейсн, — и там мы обо всем поговорили бы. Возможно, вы в итоге добьетесь желаемого результата.

— Я доложу руководству, — ответил Джереми равнодушным тоном.

Вечером я надел наушники и прослушал магнитофонную запись телефонных разговоров Блесингейма. Во время одного, едва на том конце провода сняли трубку, Джереми сказал: