Максим Кидрук - Бот

Я решил, что лабораторию будут бомбить самолеты ВВС США. Россия находится слишком далеко от Атакамы, а ни одна другая страна мира не владеет достаточно мощной стратегической авиацией. Но главное, что на сегодняшний день только у США есть бомбардировщики-невидимки, способные обмануть современные системы ПВО.

Вот так завертелась вся эта кутерьма, связанная с подготовкой операции «Антибот». Что только я не выдумывал, чтобы «B-2 Spirit» смог дотянуть до цели. Дозаправка в воздухе тоже не спасала ситуацию, ведь заправщики тоже должны были куда-то садиться. Я не знал, как быть дальше. По-голливудски взрывать лаборатории кем-то из участников проекта «NGF» не хотелось — это тривиальный, заезженный ход.

После нескольких недель кропотливого поиска неожиданно я наткнулся на статью, в которой речь шла о посадке транспортного самолета «С-130» на авианосец. Единственной в истории авиации! Выяснив, что одна из модификаций «С-130» является заправщиком, я понял, что нашел выход из тупика. Тщательно просчитав время вылета, время нанесения удара, место встречи «Призрака» с воздушным танкером и расход топлива, я «вшил» в сюжет историю о планировании операции и уничтожении лабораторий. На мой взгляд, она придала фабуле реалистичности. В любом случае выполненная работа лишней не была. Если Пентагону когда-нибудь понадобится бомбить Чили, он может использовать приведенные в романе расчеты. За точность я ручаюсь.

Не стоит, наверное, говорить, что все упомянутые в романе населенные пункты, аэропорты, пассажирские рейсы, терминалы и даже гейты также существуют.

Единственное: население Сан-Педро составляет 1938 человек. Я уменьшил его до 400 человек, чтобы с ними могли справиться 40 ботов (я рассуждал так: 3/5 из этих четырех сотен — это женщины и дети, остается 160 мужчин, разбросанных по поселку, сонных и не готовых к сопротивлению, поскольку боты пришли неожиданно среди ночи). Был, правда, другой вариант: я мог увеличить общее количество ботов и, соответственно, количество тех из них, которые сбежали, но написание современной интерпретации эпопеи «Война и мир» не входило в мои планы.

Невзирая на все вышесказанное, все герои и ключевые события романа вымышленные.

И еще… В конце лета 2011 года, написав бо́льшую часть романа, я потерял перспективу. Продолжал писать скорее по инерции, чем осмысленно. Я больше не мог объективно оценивать текст. Такое часто случается, когда пишешь большой текст. Потеря чувства новизны рано или поздно приводит к утрате веры в саму идею. Просто наступает момент, когда тебе больше неинтересно рассказывать самому себе эту историю . Это очень неприятная вещь.

Но тут я совершенно случайно наткнулся на песню «Undead» молодой rap-core-команды «Hollywood Undead». Это было настоящее землетрясение! Долбаный Везувий шарахнул огнем у меня перед мордой! Ничего подобного я не чувствовал с 1998 года, когда впервые услышал шведских рокеров «In Flames». Насыщенная импульсивная мелодия рвала меня на куски, сжигала мои внутренности. Я словно летал над землей. Этот прилив энергии надо было на что-то потратить. И я с новыми силами засел за рукопись. На рассвете каждого дня сбрасывал в плеер три песни «Hollywood Undead» — «Undead», «California» и «City» — включал звук на полную и писал, писал, писал… Никому не известные молодые рокеры стали электрошоком, который прожег мою башку, вернув в нее привычных чертиков. 6 — 7 часов / 2000 слов / 13 000 знаков каждый день — и я увидел, как отдельные оборванные куски срастаются в прочное цветное полотно, формируя целостное повествование.

Поэтому в заключение я благодарю «Hollywood Undead» за песню, которая перетряхнула стружку в моей голове и помогла закончить «Бот». Эта композиция позволит лучше понять, в каком полубезумно-эйфорическом настроении писались последние главы. Надеюсь, она пригодится и вам. Ее легко найти в Интернете. Пусть ураганные аккорды «Undead» вдохновят вас, замкнут нужные нейроны в мозгу и помогут завершить какой-нибудь проект на таком высоком уровне, на который вы только способны.

Хотя вдруг я ошибаюсь и песня не заденет ни одного из ваших жизненно важных органов?.. Ну что ж, тогда вы просто позлите ревом динамиков своих соседей. :)

М. К.

14 января 2012 года

Хостел «Cardboard Box Backpackers»

Виндхук, Намибия

P. S. Эпизод, в котором Хедхантер расстреливает ботов в самый интимный момент их короткой и такой нелегкой жизни, посвящается Квентину Тарантино и Чаку Паланику.

Перед тем как перейти к рассмотрению множества (фрактала) Мандельброта, вспомним, что такое обычное квадратное уравнение (мы все изучали их в начальных классах школы), а также то, как они решаются. Именно через такие уравнения легче всего усвоить понятие комплексных чисел и комплексной площади.

Квадратным уравнением называется алгебраическое уравнение вида:

ax 2 + bx + c = 0,

де a, b и c — коэффициенты, x — переменная.

Это уравнение имеет два решения (корня), определямые из выражения:

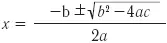
Вообще выражение b 2– 4ac, из которого добывается корень квадратный в числителе, может быть любым — как положительным, так и отрицательным. В случае b 2– 4ac ≥ 0 проблем не возникает — уравнение решается и имеет два корня. Что же получается, когда b 2– 4ac < 0, и под корнем квадратным оказывается отрицательное число? До пятого или шестого класса нас учили, что такое уравнение не решается. Корней просто не существует. Это утверждение основывалось на невозможности извлечения корня квадратного из отрицательного числа. На самом деле все совсем не так просто.

В математике немало задач, во время решения которых приходится извлекать корень из отрицательного числа. Чтобы справиться с этой проблемой, математики придумали интересную штуку, так называемую мнимую единицу. И обозначили как i = √–1 . Это число, которое, умноженное само на себя, дает минус один. То есть i 2 = –1. Таким образом, решить квадратное уравнение можно даже при b 2–4ac < 0. Корни в таком случае будут выглядеть так:

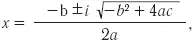
где i — мнимая единица.

А теперь забудьте о квадратных уравнениях и сконцентрируйтесь на идее мнимой единицы. Введение понятия числа i привело к появлению комплексных чисел.

В целом комплексные числа — это расширение действительных чисел, которыми мы обычно пользуемся при счете.

Любое комплексное число z записывается в виде :

z = x + iy,