Александр Дьюдни - Планиверсум. Виртуальный контакт с двухмерным миром

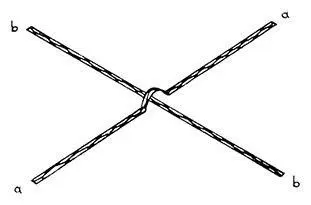
С этой проблемой легко справляется маленький набор из трех клеток. Два нервных импульса идут по волокнам А и В, но затем эти волокна расщепляются, и по каждой паре расщепленных волокон проходят копии изначального импульса.

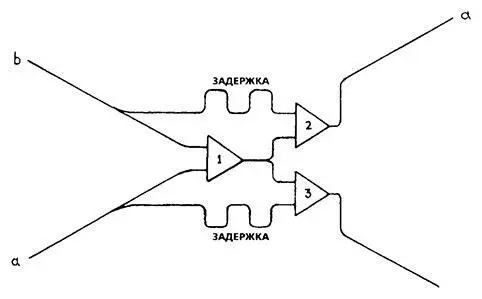
На приведенной выше схеме один из каждой пары импульсов проходит через центральную клетку (1), а второй идет в боковую клетку (2 и 3). В каждой из этих трех клеток будет сгенерирован новый импульс и направлен по выходящему нервному волокну, но только в том случае, если по любому из входящих волокон поступил только один импульс. Если в клетку одновременно поступили два одинаковых импульса, дальше они не пройдут. По такой схеме нетрудно проследить, что если нервный импульс поступил по нервному волокну а , то через долю секунды он проследует дальше по выходящему нервному волокну а . То же самое справедливо и для нервного волокна b .

То есть, какими бы возможностями ни обладали арийские нейроны, похожи они на наши или нет, они без проблем смогут взаимодействовать друг с другом. Отсутствие третьего измерения их взаимодействию не мешает. Это утверждение более двадцати лет назад оспорил ученый Г. Дж. Уитроу, заявив, что именно по этой причине в двухмерном мире не может возникнуть разум. Конечно, это была всего лишь гипотеза, причем ошибочная.

В системе Шемса всего две планеты — Арде и Нагас, и это характерный пример, демонстрирующий, что в Планиверсуме планетарные системы обычно включают в себя меньшее число планет. Большие планетарные системы могут быть нестабильными из-за свойств гравитации и большей вероятности столкновения в двухмерном мире.

Как было сказано выше, орбита Арде представляет собой самопересекающуюся кривую. Ее нетрудно изобразить на компьютере, но формулу такой кривой мы так и не получили. Орбиты небесных тел в нашей вселенной представляют собой конические сечения, а именно: окружности, эллипсы, параболы или гиперболы. Все эти кривые описываются достаточно простыми формулами. Но я не знаю, как назвать кривую, по которой Арде движется вокруг Шемса, и не знаю формулу, которая эту кривую описывает. Двое ученых из исследовательского центра IBM имени Томаса Дж. Уотсона, Джон Лью и Дональд Куорлз-младший, классифицировали орбиты планет в Планиверсуме и предложили для их описания простые приблизительные формулы, но решение уравнений для определения точной формулы оказалось дьявольски сложной задачей.

По мнению Лью и Куорлза, орбиты планет в Планиверсуме описываются тремя параметрами: фазовым углом, размером и эксцентриситетом. Первые два параметра для нас сейчас не важны, а важен лишь эксцентриситет, определяющий форму орбиты. Эксцентриситет можно вычислить, определив отношение календарного года к звездному.

Замкнутая орбита — это такая орбита, при движении по которой планета возвращается на исходную траекторию после некоторого конечного числа оборотов вокруг звезды.

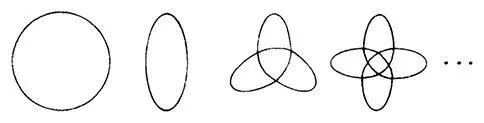
Все изображенные выше орбиты, за исключением окружности, имеют определенное количество «лепестков»: два, три, четыре и так далее. Незамкнутая орбита никогда сама себя не повторяет, и поэтому ее трудно нарисовать, ведь рисунок никогда не будет закончен. Именно по такой орбите Арде движется вокруг Шемса.

Кроме орбит, есть еще один двухмерный феномен, о котором стоило бы сказать. Раньше я утверждал, что Планиверсум представляет собой поверхность сферы, но это всего лишь предположение. На самом деле количество возможных форм Планиверсума бесконечно. Например, если Планиверсум, по выражению математиков, представляет собой ориентируемую поверхность, то он может быть либо сферой, либо подобием бублика с одним или несколькими отверстиями.

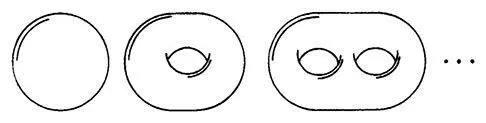
Если Планиверсум представляет собой неориентированную поверхность, то его форма может быть очень странной. Простейшая неориентируемая двухмерная вселенная — это проективная плоскость, пространство, закрученное таким образом, что если отправить жителя такой вселенной в долгое космическое путешествие, то когда он вернется, его левая и правая стороны поменяются местами. На следующем рисунке показана маленькая вселенная в форме диска, которая может оказаться проективной плоскостью.

Попробуйте пока не обращать внимание на ардийца и представьте себе, что мы можем совместить две точки А и две точки В. На самом деле мы должны совместить каждую точку на краю диска с противоположным краем, и сделать это так, как будто сшиваем весь диск, чтобы после окончания работы у диска не осталось никакого края или границы. Объект, который получится в результате, Льюис Кэрролл назвал кошельком Фортунато [3] 1 Неотения — у животных — достижение половой зрелости и окончание жизненного цикла на личиночной стадии развития. — Примеч. ред. Такое пространство очень трудно себе представить, по крайней мере, для нас, трехмерных людей, потому что его невозможно создать в трех измерениях. Для этого потребуются четыре измерения. И все-таки люди способны понять, что может произойти в таком любопытном месте. Например, мы можем представить себе, как ардиец уплывает головой вперед за край диска, глядя влево. Он пересекает край (который на самом деле невидим и неощутим) и, все еще думая, будто смотрит влево, вдруг обнаруживает, что на самом деле он смотрит вправо! Если он покинет Арде в центре такого пространства, а затем вернется, то он обнаружит, что видит мир словно в зеркальном отражении. К примеру, он больше не сможет читать пуницланские книги, но зато ваницланские прекрасно ему подойдут.

Кроме топологии имеет смысл рассмотреть и геометрию Планиверсума. Проблемы геометрии тесно связаны с тем, является ли Планиверсум открытой или закрытой вселенной. Распространенные примеры открытой двухмерной вселенной — это бесконечная плоскость и бесконечная седловидная поверхность.

Земные астрономы и космологи десятилетиями пытались выяснить, является ли наша вселенная открытой или закрытой и не свернется ли она когда-нибудь в себя. К счастью, в случае Планиверсума на второй вопрос ответить очень просто. Если, как и наша вселенная, Планиверсум возник в результате большого взрыва, он в конце концов снова схлопнется в точку. Виновницей этого финального коллапса станет двухмерная гравитация, потому что если сейчас галактики в Планиверсуме удаляются друг от друга, подчиняясь импульсу, который задал им большой взрыв, то рано или поздно они замедлят свое движение, остановятся и начнут двигаться друг к другу. Это так же верно, как и то, что ардийский космический корабль никогда не сможет покинуть гравитационное поля Арде и выйти в открытый космос. Однажды все закончится, и все галактики, Шемс и Арде, пуницлане и ваницлане, свернутся в математическую точку — к началу и к концу всего сущего.