Петр Панов - Политическая наука № 3 / 2012 г. Политические режимы в XXI веке: Институциональная устойчивость и трансформации

,

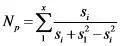где s 1– абсолютная доля голосов или мест, полученных лидирующей партией.

Однако и эта формула не позволяет отобразить с помощью ЭЧП разницу между партийными системами, в которых есть партия абсолютного большинства, и теми, где такой партии нет. Между тем эта разница принципиально важна для классификации партийных систем. Данная проблема не поддается устранению путем математической переформулировки ЭЧП. Она носит концептуальный характер: спектр возможностей ЭЧП таков, что оно подходит для измерения фрагментации, но для решения других задач нужно разрабатывать дополнительные инструменты.

В то же время математическая конструкция ЭЧП важна как методологический урок для ученых, занимающихся классификацией партийных систем. ЭЧП основано не на абсолютных, а на относительных долях мест или голосов, полученных отдельными партиями. Характерно, что преимущество такого подхода было осознано Сиароффом, который, однако, применяет его непоследовательно.

Более последовательная его реализация возможна на основе графического дизайна, который я предлагаю назвать «треугольник относительных размеров» (ТОР). В рамках этого дизайна каждой из партийных систем приписывается определенное место на сегментированной диаграмме, сегменты которой соответствуют типам партийных систем [Golosov, 2011]. Слово «треугольник» относится к тому обстоятельству, что предлагаемые координаты точек ложатся внутри ограниченного пространства, приобретающего форму равнобедренного прямоугольного треугольника:

,

,

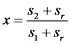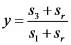где s 1, s 2, и s 3– процентные доли парламентских мест, полученные лидирующей, второй по величине, и третьей по величине партией, а s r – доля мест, совместно полученная всеми остальными партиями, начиная с четвертой по величине.

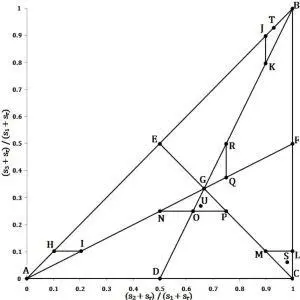
Схема 1.

Сегментированный треугольник относительных размеров

Графический дизайн ТОР представлен на схеме 1. Границами треугольника служат ось абсцисс ( AC ), линия x = 1 ( BC ), и линия y = x ( AB ), параллельная оси ординат. Геометрическим центром треугольника служит его центроид ( G ), точка пересечения медианных линий. Медианы делят треугольник на шесть равных по площади сегментов, каждый из которых соответствует одному из теоретически важных типов партийных систем. Следует отметить, что требование равновеликости сегментов, соответствующих таким типам, является принципиальным для подобных диаграмм [Comparing and contrasting the uses of two graphical tools for displaying patterns of multiparty competition, 2004].

Содержательные определения типов станут яснее, если проанализировать уравнения, которые описывают медианные линии: y = 0,5 x для AF , y = 1 – x для CE и y = 2 x – 1 для BD . Эти уравнения можно переопределить на основе введенных выше уравнений для координат. Тогда y = 1 – x оказывается эквивалентным s 1 = s 2 + s 3 + s r , что достижимо лишь при s 1 = 0,5. Значит, все точки, лежащие ниже линии CE, отображают констелляции, в которых есть партия абсолютного большинства, лежащие выше нее – те, где такой партии нет. На самой линии располагаются констелляции, в которых у лидирующей партии ровно половина мест. Сходным образом линия AF описывается как s 3 = ( s 2 – s r ) / 2, а линия BD – как s 2 = ( s 1 + s 3 ) / 2. Дальнейшие отношения между сегментами диаграммы и традиционно выделяемыми типами партийных систем не проблематичны, поскольку они однозначно характеризуются вершинами треугольника. Вершина A представляет констелляцию, в которой все места принадлежат одной партии, а это – совершенная система с доминирующей партией. Вершина C – это точка идеальной двухпартийности, поскольку здесь только две партии, у каждой из которых ровно половина мест. В точке B мы находим идеальную многопартийность, поскольку сюда попадают все констелляции, состоящие из более чем двух равных по размеру партий. Таким образом, равные по площади четырехугольные сегменты ADEG , CDFG и BEFG представляют, соответственно, системы с доминирующей партией, двухпартийные и многопартийные системы.

Каждый из этих типов разделен медианой на два подтипа. Чтобы избежать концептуальных неточностей, я присваиваю каждому из этих типов оригинальное наименование: поливалентные ( AEG ) и бивалентные ( ADG ) системы с доминирующей партией; моновалентные ( CDG ) и поливалентные ( CFG ) двухпартийные системы; бивалентные ( BFG ) и моновалентные ( BEG ) многопартийные системы. Близкие аналоги моновалентных и бивалентных многопартийных систем обнаруживаются почти во всех традиционных классификациях – у Блонделя, Уэра и Сиароффа. В первых есть партия, которая абсолютного большинства мест не получает, но все же значительно превосходит ближайших конкурентов по уровню поддержки, а во вторых существует по нескольку сопоставимо сильных крупнейших партий. Моновалентная двухпартийная система – это просто двухпартийная система в традиционном смысле слова, а поливалентная примерно соответствует «двух-с-половиной партийному» типу. В литературе обычно не проводятся различия между поливалентными и бивалентными системами с доминирующей партией, но такое различие, на мой взгляд, полезно. Об этом свидетельствует то, что ученые, которые не выделяют системы с доминирующей партией как отдельный тип, первые относят к числу многопартийных, а вторые – к числу двухпартийных, в зависимости от числа малых партий в системе.

Отмечу, что как ЭЧП является специализированным средством для измерения фрагментации, плохо подходящим для классификации партийных систем, так и ТОР имеет достаточно узкую – но именно классификационную – задачу. Аспект фрагментации он отображает весьма несовершенным образом, за счет включения в формулы величины s r , которая служит математическим пределом для величин x и y . Ни одна констелляция, в которой малые партии совместно набирают 50 % мест или более, не может располагаться на диаграмме ниже линии EF . Но при этом все без исключения констелляции, включающие более чем две равные по величине партий, оказываются в одной и той же точке, В . Таким образом, ЭЧП остается незаменимым инструментом для более точного учета фрагментации.