Питер Бернстайн - Против богов: Укрощение риска

Фридрих окружил себя ведущими интеллектуалами своего времени, пригласив многих из них к себе в Палермо. Он построил на Сицилии несколько великолепнейших замков и в 1224 году основал университет для подготовки государственных служащих — первый европейский университет, получивший устав от монарха.

Фридрих был в восхищении от книги Фибоначчи. Как-то в 1220-х годах во время визита в Пизу он пожелал его увидеть. На аудиенции Фибоначчи решал алгебраические задачи, в том числе кубические уравнения, поочередно предлагаемые ему одним из многих придворных ученых. Это побудило его написать еще одну книгу — «Liber Quadratorum», или «Книгу о квадратах», которую он посвятил императору.

Фибоначчи широко известен благодаря короткому отрывку из «Liber Abaci», содержание которого производит впечатление математического чуда. В отрывке обсуждается задача о том, сколько кроликов родится в течение года от одной пары кроликов в предположении, что каждый месяц каждая пара рождает другую пару и что кролики начинают рожать с двухмесячного возраста. Фибоначчи доказывает, что в этом случае потомство исходной пары к концу года достигнет 233 пар.

Дальше он утверждает нечто еще более интересное. Предположим, что первая пара кроликов не будет размножаться до второго месяца. К четвертому месяцу начнут размножаться их первые двое отпрысков. Коль скоро процесс продолжится, числа пар в конце каждого месяца будут такими: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233. Здесь каждое последующее число является суммой двух предыдущих. Если кролики продолжат в том же духе в течение ста месяцев, число пар достигнет 354 224 848 179 261 915 075.

Этим не исчерпываются изумительные свойства чисел Фибоначчи. Разделим каждое из них на следующее за ним. Начиная с 3, будем получать 0,625. После 89 ответ будет 0,618; с увеличением чисел в ответе будет возрастать лишь число десятичных знаков после запятой. {1} {1} Одним из удивительных свойств этих чисел является то, что число 0,618 получается, если извлечь квадратный корень из 5, который равен 2,24, вычесть 1 и затем разделить на 2; это алгебраическое выражение входит в формулу, представляющую числа Фибоначчи. .

Разделим теперь каждое число, начиная с 2, на предыдущее. Будем получать 1,6. После 144 ответ будет всегда 1,618.

Греки знали это соотношение и называли его золотой пропорцией. Эта величина определяет пропорции Пантеона, игральных карт и кредитных карточек и здания Генеральной Ассамблеи Организации Объединенных Наций в Нью-Йорке. Горизонтальная перекладина большинства христианских крестов делит вертикальную в том же отношении: длина над перекладиной составляет 61,8% от длины под пересечением. Золотая пропорция обнаруживается также в природных явлениях — в цветочных лепестках, в листьях артишока, в черешках пальмовых листьев. Отношение длины части тела человека выше пупка к длине части ниже пупка у нормально сложенного человека равно 0,618. Длина фаланг пальцев, если последовательно идти от кончиков до ладони, соотносится так же {2} {2} Точнее говоря, по формуле Фибоначчи, отношение меньшей части к большей равно отношению большей части к целому. .

Одним из наиболее романтичных воплощений отношения Фибоначчи являются пропорции и форма чудесной спирали. На приведенном рисунке видно, как она формируется на основе ряда квадратов, длины сторон которых определяются рядом Фибоначчи. Процесс начинается с построения двух маленьких квадратов одинакового размера.

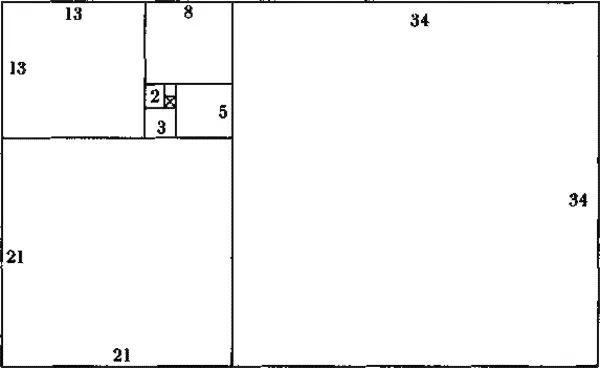
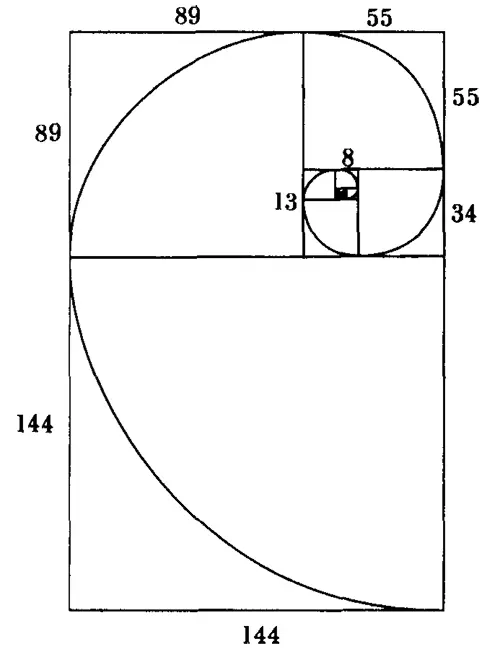
Начнем с квадрата со стороной, равной единице, пристроим к нему другой такой же квадрат, к ним пристроим квадрат со стороной, равной 2, к ним пристроим квадрат со стороной, равной 3. Продолжая в том же духе, получим квадраты со сторонами, равными 5, 8, 13, 21, 34 и так далее.

(Воспроизводится с разрешения Fascinating Fibonaccis by Trudy Hammel Garland; © 1987 by Dale Seymour Publications, P. O. Box 10888, Palo Alto, CA 94303.)

На основе двух их сторон строится примыкающий к ним квадрат со стороной удвоенного размера, затем квадраты со сторонами утроенного, упятеренного и т.д. размера. Заметьте, что таким образом строится последовательность прямоугольников, причем отношения между сторонами следующих друг за другом членов последовательности образуют золотую пропорцию. Затем соединяем противоположные углы квадратов, начиная с наименьшего, дугами, являющимися продолжением друг друга, и получаем спираль.

Нам знакома эта спираль, повторяемая в форме некоторых галактик, бараньего рога, многих морских раковин или гребешков океанских волн, по которым скользят любители серфинга. Способ построения делает ее форму неизменной, и она не зависит от размера первого квадрата, с которого началось построение: форма с ростом не меняется. Журналист Уильям Хоффер заметил: «Большая золотая спираль кажется естественным способом наращивания количества без изменения качества» [2] [2] Два комментария относительно чисел Фибоначчи и примеры взяты из: [Garland, 1987; Hoffer, 1975]. .

Кое-кто верит, что числа Фибоначчи можно использовать для различных предсказаний, в особенности относительно курса акций; такие предсказания сбываются достаточно часто, чтобы поддерживать постоянный интерес к ним. Ряд Фибоначчи настолько популярен, что в Калифорнии существует даже Американская ассоциация Фибоначчи при университете Санта-Клары, опубликовавшая с 1962 года тысячи страниц исследований по этой теме.

«Liber Abaci» Фибоначчи стала впечатляющим первым шагом на пути создания инструмента, являющегося ключом к приручению риска. Но общество еще не было готово к применению чисел для анализа связанных с риском ситуаций. Во времена Фибоначчи люди чаще связывали риск с капризами природы. Им нужно было еще научиться рассматривать его как творение рук человеческих и набраться смелости бороться с судьбой, прежде чем они смогли подойти к технологии его укрощения. Для этого понадобилось не менее двухсот лет.

Мы сможем в полной мере постигнуть значение достижений Фибоначчи, только обратив свой взгляд к эпохе, предшествующей его рассуждениям о том, как выразить различие между 10 и 100. Даже в ней мы найдем несколько замечательных новаторов.

Примитивный человек вроде неандертальца умел считать, но необходимость в счете возникала не часто. Он отмечал прошедшие дни зарубками на камнях или стволах деревьев или выкладывал дорожку камней, фиксируя число убитых животных. Время дня определялось по солнцу, и разница между пятью минутами и получасом вряд ли имела значение.