Anatoly Kondratenko - Probabilistic Theory of Stock Exchanges

To develop a probabilistic theory of the exchange, a physical method of economic research was used, the essence of which consists in using standard theoretical approaches of physics for modeling and calculating economic systems, with subsequent constant comparison of calculation results with experimental data to verify the used approaches, models and theory as a whole and for the purpose of establishing thereby the applicability limits of models and theory as a whole in those cases where their improvement and development is feasible. If the results of calculations contradict the experiment to a sufficient degree, the theory should be rejected without hesitation, and the process of theory creation should be started anew. For the sake of certainty and clarification of the theoretical problems studied in this book, we further call this option of the physical method application “a solution of the direct problem of the economic theory”, in which the results of economic activity (in this book, stock trading) are calculated based on some initial principles ( ab initio principales ), which are then compared with the corresponding experimental data (in our case – with the results of stock trading). We oppose this approach to solving, shall we say, the inverse problem of economic theory, in which by mathematical processing of experimental data one seeks to obtain information about the studied economic system. It should be said that we borrowed the terms "direct and inverse problem" from the theory of elementary particles scattering, which solves formally similar problems. It is known that solving the inverse problem in physics is very difficult and there is no reason to think that solving the inverse problem in economics will be easier. Here we reserve to developing the methods for solving the direct problem of economics as applied to stock exchanges, so all conclusions and discussions in this book refer only to the direct problem of economic theory, unless specifically stated. In order to avoid misunderstandings, we will repeatedly emphasize this aspect of this study.

It seems to us that one of the results of the extensive application of the physical method to the research of economic problems by solving the direct problem of economics will be the development of a new interdisciplinary science "physical economics", the birth of which is taking place right before our eyes. At present, physical economics is developing quite intensively in different directions, and one of these directions is probabilistic economic theory, the simplest, one may say, starting version of which is the probabilistic economics considered in this paper; and it is the latter that served as a basis for the probabilistic theory of stock exchanges. The main advantage of this approach is the availability of methods for solving the direct problem of economics, namely numerical calculations based on the first principles of such parameters and functions that can be directly compared with Experimental data, in our case – with the experimental results of real-time exchange trading.

According to the new physical method of thinking and research in economics, which we share and develop, in this monograph as well, the main requirement to such economic models, defining their main purpose, is the possibility and, to some extent, even art, with a few important axioms, concepts and principles to harmoniously, competently and simultaneously include them in the theory. The latter is very important, since, by the definition of the purpose, all concepts and principles play certain roles of comparable importance in the studied economy. And of course, constant verification of the assumptions made, concepts and the theory itself through numerical calculations and comparison with experiment data is necessary. It is this emphasis on experimental verification of theories that distinguishes the physical method from all other approaches, including neoclassical theory, which is currently mainstream in economics. In other words, the physical method of economic research presupposes a constant reliance on experiment, as it is usually the case in physics: numerical solutions of a direct problem are compared with the corresponding experimental data. We are fully confident that due to its naturalness and obviousness, in the nearest future the physical method will become the main method of economic research, will be called simply a scientific method of economic research, so the necessity to call it a physical method in economics will disappear due to irrelevance and unnecessity.

It is well known that the method of conceptual modeling of economic systems has long been widely used in economic theory. For example, the first and most famous concepts of neoclassical economics are S&D concepts. It is due to them that neoclassical theory has made a significant contribution to economic science. It helped economists better understand the basic components of the economic world, and with the help of a graphical interpretation this knowledge became more accessible to those interested in these issues, in particular students. In Austrian economics, the so-called method of ideal or imaginary constructions rightfully occupies one of the central places [Mises, 2005].

It is not customary in theoretical physics to emphasize the use of models, since theoretical physics itself can rightly be viewed as a conceptual mathematical modeling of physical systems. In particular, theoretical physics has developed the most advanced methods of theoretical modeling of complex systems. Moreover, here it has long been implicitly required from the researcher to perform quantitative numerical calculations of the structure and properties of such models with the highest possible accuracy, which, in turn, led to a striking development of quantitative methods in quantum mechanics of multiparticle systems, especially in quantum chemistry of multi-atom systems [Kondratenko and Neyman, 1990].

So, in this study deep structural and dynamic analogies between physical multi-atom systems and multi-agent economic systems are used in order to transfer conceptual, analytical and numerical methods from theoretical physics to theoretical economics. This transfer is performed by means of physical modeling of economic systems or, in short, physical-economic modeling. Our concept of physical-economic modeling is based on the well-known fundamental ideas of classical economic theory, first of all of Austrian economics. They are then combined and eventually, with the help of additional concepts and mathematical body adopted from physics, transformed into a new economic theory. This combination is organized through formal approaches and methods borrowed from theoretical physics, starting from the introduction into economic theory of the formal economic space concepts, motion trajectories of market agents and the market as a whole in such space, and finishing with the substantiation of the principal possibility of using the method of equations of motion in economic theory. To avoid misunderstandings, we emphasize again that the role of theoretical physics here is only to provide the mechanisms for developing a probabilistic economics. Relying on this theory, step by step, taking into account all principles of the theory simultaneously, we create more complex physico-economic models, taking into account the experience with previous models, which will be repeatedly illustrated in figures and graphs.

Of course, all physical-economic models are essentially conceptual mathematical models, just as in physics. The notion of "physical modeling" is used to emphasize an analogy with the rules or principles of modeling in physics. Further, this term will become redundant and will not be used. In the course of developing conceptual models of economic systems we will consistently introduce the concepts and principles of our theory, which will serve as a basis for the models’ frameworks, which, in turn, will be filled with new content step by step. We will start with constructing the simplest models with the help of analogies and formal methods of classical mechanics. For the sake of brevity, we will call such models classical models below. Naturally, only the first five principles will be used in the development of such a classical theory, or simply classics, since only they have analogues in classical mechanics.

So, Fig. 1.1 shows a typical graphic economic model of a market system, or simply, a market. This model, configured by analogy with models for physical multiparticle systems, uses a number of legends or conventions to demonstrate typical market structure.

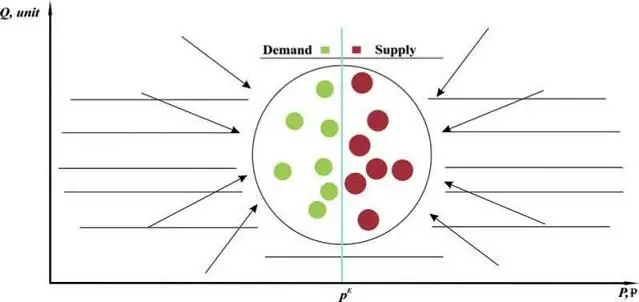
Fig. 1.1. Graphical model of a single-commodity multiagent market economy in the economic two-dimensional price-quantity space. The dots inside the conventional sphere represent market agents: buyers (green dots) and sellers (red dots), forming demand and supply, respectively. The sphere is divided into two parts by the narrow blue line, which symbolically marks the narrow area of prices, where the transactions in the market are made at the current experimental price p Exp . Buyers are in the left hemisphere and sellers are in the right hemisphere, since the buyers’ prices are lower than the sellers’ prices with very rare exceptions.

The main structural element of the model is the market itself, consisting of a certain number of interacting market agents: buyers and sellers. This market is not a closed system – it is an open system, because it is under the constant influence of its institutional and external environment, as well as other markets and other sources of influence. All these factors also serve as structural elements of the market, because they exert a strong influence on market agents, and without taking it into account it is impossible to obtain a reliable description of the mechanisms of market operation and its results.

Further, in order to be able to mathematically describe the dynamics of the economy, we should, just like in physics, place the entire market into some constructed economic spaces. Since such economic spaces, in contrast to the physical space, have an auxiliary and formal character, they can be constructed in different ways depending on the tasks to be solved. In this paper, it is appropriate to use the price-quantity space corresponding to two sets of independent variables, prices P and quantities Q for all traded goods on the market ( PQ -space). For clarity, we denote the names of independent variables and their corresponding coordinate axes in bold. Despite its seeming simplicity, the concept of multidimensional economic space introduced in this study is of great importance in theory, since it provides a fundamental opportunity to describe the dynamics of economic systems in mathematical and graphical languages, as it has long been accepted in science.

This paper will extensively use the notion of "market structure", which includes both the agent structure of the market itself and all significant external factors and forces of various nature that affect the operation of the market. The study of the market structure and its various microstructures and the identification of the most important characteristics and connections between them represents the most important purpose of any economic theory.

The approach of probabilistic economics, aimed at solving the problem of adequate quantitative description of each agent’s behavior in the market, as well as the behavior of the market as a whole, is based on one rather simple premise or hypothesis, which we will call an axiom. This axiom, which has a rather general character, forms the basis for the implementation of supply and demand concept in a probabilistic economy.