Денис Шевчук - Как играть на российских биржах

• Обеспечивает максимальную ожидаемую доходность для некоторого уровня риска.

• Обеспечивает минимальный риск для некоторого значения ожидаемой доходности.

Набор портфелей, удовлетворяющих этим двум условиям, называется эффективным множеством ( efficient set ).

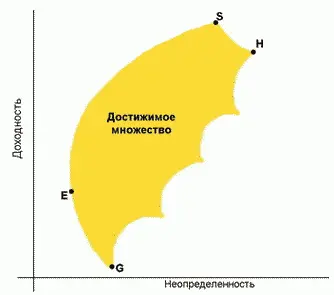
Достижимое и эффективное множества

Рисунок 1 представляет иллюстрацию местоположения достижимого множества ( feasible set ), также известного как множество возможностей, из которого может быть выделено эффективное множество. Достижимое множество представляет собой все портфели, которые могут быть сформированы из группы N ценных бумаг. Это означает, что все возможные портфели, которые могут быть сформированы из N ценных бумаг, лежат либо на границе, либо внутри достижимого множества (точки G, E, Sи Hна рис.1 являются примерами таких портфелей). Определим местоположение эффективного множества. Множеством портфелей, обеспечивающих максимальную ожидаемую доходность при изменяющемся уровне риска, является часть верхней границы достижимого множества, расположенная между точками Eи H. Множеством портфелей, обеспечивающих минимальный риск при изменяющемся уровне ожидаемой доходности, является часть левой границы достижимого множества, расположенная между точками Sи G. Учитывая, что оба условия должны приниматься во внимание при определении эффективного множества, отметим, что нас удовлетворяют только портфели, лежащие на верхней и левой границе достижимого множества между точками Eи S. Соответственно эти портфели составляют эффективное множество, и из этого множества эффективных портфелей ( efficient portfolios ) инвестор будет выбирать оптимальный для себя. Все остальные достижимые портфели являются неэффективными портфелями ( inefficient portfolios ), поэтому мы их можем игнорировать.

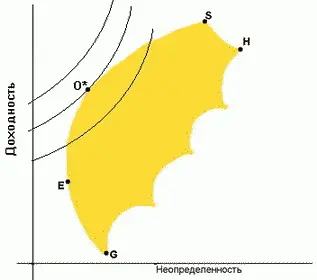
Выбор оптимального портфеля

Каким образом инвестор выбирает оптимальный портфель ( optiтal portfolio )? Как показано на рис.2 инвестор должен нарисовать свои кривые безразличия на одном рисунке с эффективным множеством, а затем приступить к выбору портфеля, расположенного на кривой безразличия, находящейся выше и левее остальных. Этот портфель будет соответствовать точке, в которой кривая безразличия касается эффективного множества. Как видно из рис.2, таким портфелем является портфель O*на второй кривой безразличия . Несомненно, что инвестор предпочел бы портфель, находящийся на первой кривой (выше и левее), но такого достижимого портфеля просто не существует.

Марковиц разработал очень важное для современной теории ценных бумаг положение, которое гласит: совокупный риск портфеля можно разложить на две составные части. С одной стороны, это так называемый систематический риск, который нельзя исключить и которому подвержены все ценные бумаги практически в равной степени. С другой – специфический (несистематический) риск для каждой конкретной ценной бумаги, который можно избежать при помощи управления портфелем ценных бумаг (диверсификации). Одной из основных идей диверсификации при инвестировании является эффект отрицательной коррелированности, называемый также эффектом Марковица: при составлении портфеля ценных бумаг надо стремиться к тому, чтобы вложения делались в бумаги, среди которых, по возможности, много отрицательно коррелированных. Другая идея – это эффект некоррелированности: если инвестирование производится в некоррелированные ценные бумаги, то для уменьшения риска надо, по возможности, брать их число как можно большим.

В предыдущей статье был описан подход к формированию портфеля, предложенный Марковицем. Подход Марковица предполагает, что активы, рассматриваемые для инвестиций, являются рисковыми, т.е. каждый из рисковых активов дает неопределенный доход. Поскольку никакой из активов не имеет совершенно отрицательную корреляцию с любым другим активом, то все портфели также дают неопределенные доходы за период владения и, следовательно, являются рисковыми. Более того, инвестору не позволяется использовать оодлженные деньки вместе с начальным капиталом для покупки портфеля активов. Это означает, в модели Марковца инвестору не разрешается использовать финансовую поддержку или счет, находящийся у его брокера. В этой статье мы рассмотрим подход, который обобщает модель Марковица. Этот подход был предложен Джеймсом Тобином в работе «Национальная экономическая политика» (1966). Тобин показал, что для того, чтобы добиться сбалансированности в своих инвестиционных портфелях, инвесторы стремятся сочетать инвестиции с повышенной степенью риска с менее рискованными, которые в настоящее время принято называть безрисковыми активами. Итак, под безрисковым активом понимается ( riskfree asset ) такой актив, будущая стоимость которого определена в любой момент времени. Если инвестор покупает безрисковый актив в начале инвестиционного периода, то он точно знает, каковым будет его доход в конце периода. К таким активам можно отнести казначейские ценные бумаги и государственные облигации со сроком погашения, совпадающим с периодом владения, банковский депозит и кредит, а также с некоторой долей условности корпоративные облигации. Чтобы ценная бумага действительно была безрисковой, по ней не должны осуществляться купонные выплаты в течение владения этой бумагой инвестором. Она должна обеспечить ему единоразовую выплату в последний момент владения. Любые промежуточные купонные выплаты подвергнут инвестора риску ставки реинвестирования, поскольку он не знает ставки, по которой могут быть реинвестированы купонные выплаты на остаток периода владения. С появлением на рынке безрискового актива инвестор получит возможность вкладывать часть своих денежных средств в этот актив, а остаток – в любой из рисковых портфелей, содержащихся в множестве достижимости Марковица. Появление новых возможностей существенно расширяет достижимое множество и, что важнее, изменяет расположение значительной части эффективного множества Марковица.

Можно показать, что любая комбинация из безрискового и рискованного актива будет лежать на прямой линии в координатах неопределенность-доходность. Точное положение точки будет зависеть от пропорции инвестиций в эти два актива. Рассмотрим сочетание безрискового актива и рискованного портфеля, достижимое множество в этом случае будет иметь вид, показанный на Hисунке 1. В частности, обратите внимание на то, что две границы являются прямыми линями, выходящими из точки, соответствующей доходности безрискового актива. Нижняя линия соединяет две точки, соответствующие безрисковому активу и низкорисковой акциям достижимого множества Марковица. Поэтому она определяет портфели, являющиеся комбинациями низкоризковой акции и безрискового актива.