Сборник - Леонардо да Винчи. Избранные произведения

Монджибелла – Этна. Это одно из немногих мест, в которых Леонардо касается вулканических извержений. Поскольку жизнь Леонардо протекала в Северной Италии, он не имел случаев наблюдать их и сосредоточить на них свое научное внимание. Ср. о «нептунизме» Леонардо примеч. 371— 372.

Волнение перед еще неразгаданным ( 51) уживается с ясным пафосом математизма ( 52— 53). Задача удвоения куба ( 54) дает Леонардо повод сказать о природе геометрии. Квадратура секторов круга – характерный пример того, как им трактуются математические задачи ( 55— 56). И «раем математических наук» является механика ( 57), наука благороднейшая и наиполезнейшая ( 58).
Все подчинено числу, и законы пропорции мы найдем всюду ( 59— 60). Леонардо хочет измерить и сосчитать то, чего не измеряли и не считали древние: силу света ( 61), силу зрительной способности ( 62), «силу» цвета ( 63), скорость ветра ( 64), приборами измерить дальность пути, совершенного путником ( 65), повозкой ( 66), кораблем ( 67). Он хочет измерить силу удара ( 68), влажность воздуха ( 69) и удаленность грозы ( 70).

Арабский философ и ученый аль-Кинди в своем трактате о пропорциях, известном Леонардо, утверждал, что философия не может быть постигнута без математики. Имя аль-Кинди пользовалось большим уважением в среде ученых, окружавших Леонардо, в частности у Фацио Кардано, отца знаменитого математика. Сближение с известным изречением Платона, возбранившего в свою школу вход не знающим геометрии, было бы поверхностным. Математизм Леонардо – не математический идеализм Платона и платоников, у которых (в особенности в позднем платонизме) математизм окрашен теологически. Но это и не математическая философия классического периода новой философии с ее апофеозом «геометрического» метода. Леонардо ставит акцент не столько на строгости и стройности математических доказательств, доказательств more geometrico, сколько на моментах арифметического счета и эмпирико-физических измерений.

Об универсальной приложимости математики говорит в своем трактате о гражданской и военной архитектуре Франческо ди Джорджио Мартини (1425–1506), с которым в 1490 г. Леонардо находился в Милане и Павии на службе у Лодовико Моро. Любопытно (но не более) сравнить это высказывание Леонардо с высказыванием Канта в его «Метафизических началах естествознания»: «Я утверждаю, что в каждой специальной естественной науке можно найти собственно науки лишь столько, сколько в ней математики».

Диагональные сечения кубов соответственно равны a 2√2 и b 2√2. По Леонардо, 2 a 2√2 = b 2√2, откуда b = a √2 тогда как на самом деле b = a 3√2.
…квадрат – т. е. четырехугольник.
…делосцам . – Имеется в виду сказание о жителях острова Делос, во время моровой язвы получивших указание от оракула удвоить кубический жертвенник Аполлона и за разрешением задачи обратившихся к Платону и его ученикам. Отсюда частое обозначение задачи удвоения куба как «делосской». По словам Плутарха (Quaest. conv. VIII, 2, I), Платон порицал Эвдокса, Архита и Менехма за то, что они прибегли к инструментальным и механическим способам решения задачи и этим низвели геометрию от идеального к чувственному. Способ Платона до нас не дошел; приписываемый ему (у Евтокия Аскалонского) как раз пользуется инструментально-механическими приемами. В «Тимее» (31 b и сл.) видно, однако, знакомство с задачей двух средних пропорциональных, к которой, в сущности, и сводится задача удвоения куба:

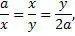
откуда x 3= 2a 3 .

Этот и следующий отрывок особенно характерны для леонардовского способа решения математических задач. При большой, так сказать, зрительно-мускульной наглядности – равнодушие к четкости и заостренности словесного выражения.