Юрченко Борисович - Философия и логика времени

Чтобы нарисовать циркулем окружность, нам нужно время. Только всемогущий ум, по мнению Больцано, может при этом обойтись без времени. Пусть имеется прямая в Евклидовом 3-мерном пространстве. Будем вращать ее вокруг произвольного центра О с любой угловой скоростью. Очевидно, что на некотором расстоянии R от центра О скорость точки R(x) достигнет световой. Эта скорость есть первая производная координаты, но у нее не может быть второй производной, а именно: ее ускорение есть само время, т.е. абсолютный покой. Это значит, что на нее не действуют никакие силы, ее движение инерциально и происходит по траектории нулевой кривизны, которая тем не менее оказывается замкнутой. Точка R ( x ), можно сказать, одновременно охватывает собою все точки окружности или, наоборот, вся окружность стягивается в эту точку покоя с бесконечной положительной кривизной, образуя петлю времени. Это – фотон, с массой 0 и спином , будто мнимым квантом действия . Полученный радиус определит световую сферу, но поскольку точка R(x) становится световой, т.е. эфирной, то мы вправе считать ее радиусом Хаббла.

Для математического описания вращающейся окружности или (в более общем случае) диска используются координаты Борна. Метрика здесь такова:

где R есть радиус окружности, – положение точки на окружности и – круговая частота, .

Геометрия такого вращения не является ортогональной и создает, как известно, множество принципиальных трудностей в непротиворечивом определении собственного времени уже при попытке мысленной синхронизации часов. Опуская формализм, это можно объяснить так. Пусть R(t ) есть равномерно скользящая во времени точка радиуса. Примем ее за элементарную частицу (фермион). В пространстве Минковского М мировая линия этой «t-подобной» частицы будет винтовой, образуя конус. Иначе говоря, в факторизованном пространстве M/t эта частица в каждый квант времени будет переходить из страты в следующую страту , не создавая замкнутую окружность. Она образует замкнутую окружность лишь при достижении скорости света, полностью уместившись в одну страту как петля времени. При этом, согласно лемме 10, «t-подобный» фермион должен превратиться в «s-подобный» бозон, перейдя из гиперболоида (или ) в гиперболоид на рис. 12.

Если связать точку с ИСО, которая вращается вместе с ней, то траектория этой точки в ней будет логарифмической, как в истории Ахиллеса-Орфея, падающего из точки мгновенного покоя в абсолютный покой, который в данном случае с вращающейся точкой охватит собою всю окружность, а по сути всю страту, в которой образуется замкнутая временная петля. Именно таковым должен быть горизонт событий черной дыры.. Любое физическое тело на горизонте событий, согласно гипотезе Сасскинда и его коллег [42], при использовании принципа комплементарности в корпускулярно-волновом дуализме КМ, должно разложиться в голограмму на «растянутом горизонте». Этот горизонт является мембраной, расположенной на расстоянии Планковской длины от горизонта событий, т.е. эта «мембрана» играет ту же роль, что и t-подобный гиперболоид над световым конусом будущего. Для внешнего наблюдателя, падающая информация нагревает растянутый горизонт и отражается от него в качестве излучения Хокинга, сохраняя унитарность информации.

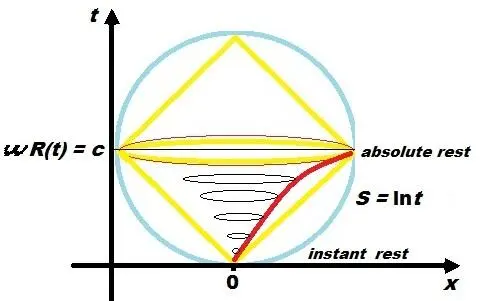
Рис.23

В нашем понимании здесь хронодинамика сходится с термодинамикой, поскольку черные дыры образуют состояние вещества, близкого к температурному и временному абсолютному нулю. Можно ли предположить, что черные дыры образуют некий «конденсат Бозе-Эйнштейна»? Ведет ли себя черная дыра как единая суперчастица между прошлым и будущим в s-подобном гиперболоиде ? Являясь единым телом, она должна быть связанной во времени структурой, но при этом, будучи суперчастицей-бозоном, не выходить за пределы , «растягивая» его. (Очевидно, в подходящем формализме этот «конденсат» можно описать в виде единой «струны», как это допускается в теории струн.) И тогда черные дыры испаряются одновременно сразу во Вселенную и в анти-Вселенную, так что белые дыры, получающиеся из них обращением времени, оказываются иллюзорным формализмом. Их попросту не может быть, поскольку черные дыры t -симметричны. К вопросу о потери информации в черных дырах мы вернемся позже, связав ее естественным образом с проблемой «голой сингулярности» и соответственно с кривизной пространства.

Самым важным для нас здесь является то, что замкнутую окружность невозможно получить как непротиворечивую мировую линию в М . Получить ее можно только как s-подобную временную петлю. Между тем она кажется нашему мозгу совершенно естественной фигурой в евклидовой (и вневременной) геометрии. Окружность, нарисованная нами на листе, есть такая же геометрическая химера, как замкнутая лестница, идущая все время на спуск (рис.3). Как сказано в самом начале нашего исследования, все фотографии лгут. Нарисовать замкнутую окружность можно только в абсолютном покое как петлю времени. Физически это невозможно. Идею числа π мы извлекаем именно из этой химеры. Но это может значить, что это число связано с кривизной физического реального пространства.

Что может значить для нас модель сферического пространства, в котором ? Во-первых, это значит, что Вселенная замкнута, ее полная энергия равна нулю, а ее границей является глобальный горизонт. Точка (фермион), достигнув световой скорости, становится бозоном, образующим в страте временную петлю с радиусом, но при световой скорости петля оказывается безразмерной:

В этом случае Вселенная является открытым топологическим пространством, а глобальный горизонт – ее сингулярным замыканием.

Нет смысла говорить о том, что происходит на границе световой сферы, поскольку там начинается неполнота нашего самосознания. Эта граница пространства и есть чистое время. По сути – это число π. Но это число применимо к любой точке внутри радиуса, так что сфера не имеет фиксированного пространственного размера, и поэтому световая точка заполняет собою всю сферу. Действительно, любая точка внутри , включая центр вращения, в мгновенном покое оказывается световой, поскольку все пространство Минковского вне времени есть эфир. Если мозг находится внутри сферы, ее граница становится для него глобальным горизонтом Вселенной, им порожденной. Если он снаружи, то она оказывается горизонтом событий черной дыры, где ему нет места.

Из уравнения (7.4) следует, что Вселенная состоит из суммы 3-мерных пространств, а лемма 9 говорит, что эти пространства сохраняются лишь в нашей памяти, в действительности же Вселенная сводится к одной-единственной страте, т.е. к суперпозиции двух страт. Т.о. любая точка на сфере горизонта есть «фокус выворачивания» мира в антимир, так что световую сферу можно считать гиперплоскостью зазеркалья со сверхсветовыми скоростями.