Стивен Строгац - Удовольствие от Х

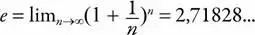
Это наиболее существенный вычислительный аргумент в пользу числа е . Как говорилось в предыдущих главах, где мы вычисляли площадь круга и размышляли о притяжении Земли к Солнцу, дифференциальное и интегральное исчисления, основанные на исчислении бесконечно малых, от других разделов математики отличаются тем, что стремятся обуздать ужасающую власть бесконечности. Имея дело с пределами производных или интегральных сумм, необходимо всегда очень осторожно подходить к бесконечности.

В процессе приближения к пределу, который вел к e, мы разделили год на все возрастающее число периодов начисления сложных процентов. Можно сказать, разбили его на временн ы е окошки, которые становились все у же и у же, и в конечном счете подошли к тому, что можно описать как бесконечное множество бесконечно узких окошек. Забавно, что чем чаще в течение определенного периода начисляется процент по вкладу, тем медленнее растут деньги. Тем не менее через год по-прежнему набегает приличная сумма процента, потому что он многократно умножался на протяжении бесконечно многих периодов!

Таков ключ к вездесущности e . Оно часто возникает, когда что-то меняется в результате суммарного действия множества крошечных воздействий.

Рассмотрим кусочек урана в процессе радиоактивного распада. Момент за моментом каждый атом имеет определенный маленький шанс подвергнуться распаду. Произойдет ли это с каждым из них и когда — совершенно непредсказуемо, и каждое такое событие оказывает в целом бесконечно малое влияние. И все же в совокупности эти триллионы событий создают сглаженный, предсказуемый, экспоненциально затухающий процесс радиоактивного распада.

Или подумайте о населении Земли, которое растет в геометрической прогрессии. Во всем мире дети рождаются в случайных местах в непредсказуемые моменты, пока другие люди умирают тоже в случайных местах в непредсказуемые моменты. Каждое событие имеет мизерное в процентном отношении воздействие на демографическую ситуацию в мире, но в совокупности население растет в геометрической прогрессии с очень предсказуемой скоростью.

Есть еще одна причина для появления e , сочетающая в себе огромное число вариантов выбора. Для ее иллюстрации приведу два примера из повседневной жизни, хотя и в очень стилизованной форме.

Представьте себе, что популярный новый фильм показывают в местном кинотеатре. Это романтическая комедия, и сотни пар (намного больше, чем может вместить кинотеатр) выстроились в кассу в очередь за билетами, хотя и отчаялись попасть внутрь. Как только счастливая пара получает билеты, она пробирается в зал и ищет два места рядом. Для простоты предположим, что влюбленные выбирают эти места наугад, там, где есть свободные. Другими словами, они не заботятся о том, будут ли сидеть близко к экрану или далеко от него, на проходе или в середине ряда. Пока они рядом друг с другом, они счастливы.

Допустим, ни одна пара не будет пересаживаться, чтобы освободить место для другой. После того как молодые люди уселись, они никуда не передвигаются. Полное отсутствие вежливости. Зная это, кассир прекращает продавать билеты после того, как остается только одно свободное место. В противном случае начались бы драки.

Сначала, пока в кинотеатре довольно пусто, не возникает никаких проблем. Каждая пара легко находит два места рядом. Но через какое-то время остаются только одиночные места и одиночные промежутки между парами, которые двое не хотят занимать. В реальной жизни люди часто намеренно создают такие промежутки: чтобы положить пальто или не опираться на один подлокотник с неприятным незнакомцем. Но в нашей модели эти промежутки случайны.

Вопрос: если больше не осталось мест для пар, сколько свободных мест еще есть в кинотеатре?

Ответ следующий: оказывается, в кинотеатре с большим залом (когда в ряду много мест) доля пустующих мест примерно равна

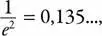
что приближается к 13,5%72.

Хотя сам расчет слишком сложный для того, чтобы его здесь привести, легко заметить, что 13,5% находится в правой части диапазона между двумя крайними значениями. Если бы все пары сидели вплотную друг к другу, пустующих мест не было бы.

Тем не менее, если бы они расположились максимально нерационально , то есть всегда оставляя возле себя свободное место (и оставив свободное место в каждом ряду у прохода: на одном или на другом конце ряда, как показано на рисунке ниже), то пустовала бы одна треть мест, потому что каждая пара заняла бы три места: два для себя и одно промежуточное.

Догадываясь, что произвольный выбор должен лежать где-то между идеально рациональным и совершенно неэффективным, иначе говоря, быть средним между 0 и 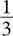, мы ожидаем что-то около , то есть что 16,7% мест будут пустовать. И это недалеко от точного результата 13,5%.

Здесь большое число вариантов возникло из-за того, что у пар был богатый выбор в огромном кинотеатре. Наш следующий пример тоже об организации пар, только теперь не в пространстве, а во времени. То, о чем я говорю, касается довольно болезненной проблемы: со сколькими партнерами я должен встретиться прежде, чем выберу себе супругу73. Реальный вариант этой задачи слишком сложен для математического расчета. Рассмотрим упрощенную модель. Несмотря на допущения, невозможные в жизни, в ней все еще сохраняется некоторая душераздирающая романтическая неопределенность.

Предположим, вам известно, сколько потенциальных супругов вы встретите в течение жизни. (Фактическое количество не важно, лишь бы знать наперед, сколько их будет, и чтобы не слишком мало).

Предположим также, что вы могли бы оценить этих людей однозначно (то есть выбрать наилучшего), если бы увидели их всех вместе. К несчастью, это невозможно. Вы встречаете их только по одному и в случайном порядке. Таким образом, вы не можете знать, находится ли предмет ваших мечтаний с первым номером из вашего списка прямо за углом или вы уже встречались и расстались.

И правила этой игры таковы: как только вы позволите кому-то уйти, он (или она) тут же уходит. Второго шанса нет.

Наконец представим, что вы хотите остепениться. В этом случае, если вы порываете с тем «наилучшим на сегодняшний день», кого в прошлом не поместили в верхнюю часть списка, вы будете считать свою личную жизнь неудачной.