Стивен Строгац - Удовольствие от Х

Хотя приведенные примеры фантастические, описывающие их типы уравнений весьма содержательны. Они представляют собой наиболее мощные инструменты из когда-либо созданных человечеством для осмысления материального мира. Сэр Исаак Ньютон использовал дифференциальные уравнения для открытия тайны движения планет. С помощью этих уравнений он объединил земные и небесные сферы, показав, что и к тем и к другим применимы одинаковые законы движения.

Спустя почти 350 лет после Ньютона человечество пришло к пониманию того, что законы физики всегда выражаются на языке дифференциальных уравнений. Это верно для уравнений, описывающих потоки тепла, воздуха и воды, для законов электричества и магнетизма, даже для атома, где царит квантовая механика.

Во всех случаях теоретическая физика должна найти правильные дифференциальные уравнения и решить их. Когда Ньютон обнаружил этот ключ к тайнам Вселенной и понял его великую значимость, он опубликовал его в виде латинской анаграммы. В вольном переводе она звучит так: «Полезно решать дифференциальные уравнения»75.

Глупая идея описать любовные отношения с помощью дифференциальных уравнений пришла мне в голову, когда я был влюблен в первый раз и пытался понять непонятное поведение моей девушки. Это был летний роман в конце второго курса колледжа. Я очень напоминал тогда первого Ромео, а она — первую Джульетту. Цикличность наших отношений сводила меня с ума, пока я не понял, что мы оба действовали по инерции, в соответствии с простым правилом «тяни-толкай». Но к концу лета мое уравнение начало разваливаться, и я был еще более озадачен. Оказалось, произошло важное событие, которое я не учел: ее бывший возлюбленный захотел ее вернуть.

В математике мы называем такую задачу задачей о трех телах. Она заведомо неразрешима, особенно в контексте астрономии, где впервые и возникла. После того как Ньютон решил дифференциальные уравнения для задачи о двух телах (что объясняет, почему планеты движутся по эллиптическим орбитам вокруг Солнца), он обратил внимание на задачу о трех телах для Солнца, Земли и Луны. Ни он, ни другие ученые так и не смогли ее решить. Позже выяснилось, что задача о трех телах содержит семена хаоса76, то есть в долгосрочной перспективе их поведение непредсказуемо.

Ньютон ничего не знал о динамике хаоса, но, по словам его друга Эдмунда Галлея[29], пожаловался, что задача о трех телах «вызывает головную боль77 и так часто не дает ему спать, что он больше не будет об этом думать».

Здесь я с вами, сэр Исаак.

21. Выйди на свет[30]

Господин Дикурцио был моим наставником в средней школе — хмурый и требовательный, склонный к сарказму человек, носивший скучного вида очки в черной оправе. Словом, симпатяга. Но я заметил его безумную страсть к физике.

Однажды я рассказал ему, что прочитал биографию Эйнштейна. В ней говорилось, что во время учебы в колледже Эйнштейн был сильно поражен чем-то под названием «уравнения Максвелла для электричества и магнетизма»; и я заявил, что не могу ждать, пока начну достаточно разбираться в математике, чтобы узнать, что они собой представляют.

Это произошло во время ужина в школе-интернате. За большим столом сидели еще несколько студентов, жена учителя и две его дочери; господин Дикурцио раскладывал картофельное пюре по тарелкам. При упоминании об уравнениях Максвелла он бросил ложку, схватил бумажную салфетку и начал писать на ней загадочные символы, точки и кресты, перевернутые треугольники, E и В со стрелками над ними, и вдруг, как мне показалось, он заговорил на нечеловеческом языке: «Ротор ротора — это градиент дивергенции минус квадрат дельты...»

Что за абракадабру он бормотал? Теперь-то я понимаю, что он давал объяснения в терминах векторного исчисления78 — раздела математики, описывающего все находящиеся вокруг нас невидимые поля. Вспомните магнитное поле, поворачивающее стрелку компаса на север, гравитационное поле, притягивающее ваш стул к полу, или микроволновое поле, которое готовит ваш ужин.

Наибольшие достижения векторного исчисления лежат в том сумеречном мире, где математика сталкивается с реальностью. В самом деле, история Джеймса Максвелла и его уравнений показывает один из сверхъес­тественных случаев несомненной эффективности математики. Так или иначе, перетасовав несколько символов, Максвелл обнаружил, что такое свет79.

Чтобы осознать значимость его открытия и получить общее представление о векторном исчислении, давайте начнем со слова «вектор». Оно происходит от латинского корня vehere , «осуществлять», который также дает нам такие слова, как «транспортное средство» (vehicle) и «лента конвейера» (conveyor belt). Для эпидемиологов вектор является носителем возбудителя, подобно комару, передающему малярию через кровь. Для математика вектор (по крайней мере в своей простейшей форме) — это шаг, который переносит вас из одного места в другое.

Вспомните одну из схем для начинающих танцоров бальных танцев, покрытую стрелками, указывающими, как, танцуя румбу, ставить правую ногу, а затем левую:

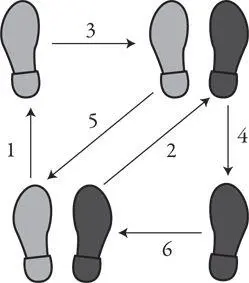
Эти стрелки и есть векторы. Они содержат два вида данных: направление (в каком направлении переставлять ногу) и величину (на какое расстояние ее нужно переместить). Все векторы имеют такую двойственность.

Векторы, как и числа, можно складывать и вычитать, но наличие направленности делает их более сложными. Тем не менее сложение векторов становится более понятным, если вы представите его в виде инструкции по танцам. Например, что получится, если сначала вы делаете один шаг на восток, а следующий на север? Естественно, вектор, который указывает на северо-восток.

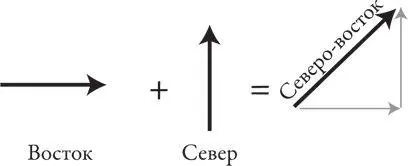
Примечательно, что скорость и сила ведут себя так же: они складываются, как и танцевальные шаги. Это должно быть знакомо любому теннисисту, который когда-либо пытался подражать Питу Сампрасу и бил по мячу справа снизу от линии, когда бежал на полной скорости к боковой линии. Если направить мяч без учета своего движения, то удар будет неточным. Скорость мяча по отношению к корту — это сумма двух векторов: скорости мяча относительно вас (вектор, направленный снизу от линии, как и предполагалось) и вашей скорости относительно корта (вектор, направленный в ту сторону, куда вы бежите). Чтобы отбить мяч в нужном направлении, необходимо целиться в противоположную половину поля противника, чтобы компенсировать боковое движение.