Стивен Строгац - Удовольствие от Х

Возьмем, к примеру, распределение размеров городов в США. Вместо того чтобы скапливаться вокруг некоей средней величины колоколообразной кривой, подавляющее большинство городов имеют небольшой размер и, следовательно, скапливаются в левой части графика.

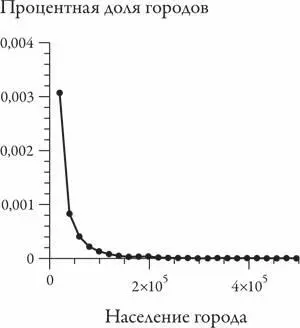
И чем больше население города, тем реже такие города встречаются. Иначе говоря, в совокупности распределение будет представлять собой скорее кривую в форме буквы L, чем колоколообразную кривую.

И в этом нет ничего удивительного. Все знают, что мегаполисов гораздо меньше, чем маленьких городов. Хотя это не так очевидно, размеры городов подчиняются простому красивому распределению — если посмотреть на них в логарифмическом масштабе.

Будем считать, что различие между двумя городами одно и то же, если их население отличается в одно и то же число раз (подобно тому как две любые клавиши рояля, отстоящие на октаву, всегда разнятся вдвое по частоте). И сделаем то же самое на вертикальной оси.

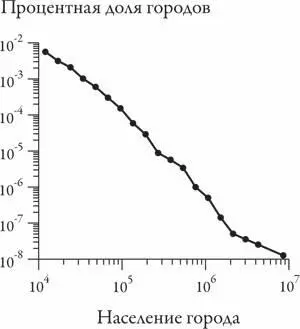
Теперь данные располагаются на кривой, представляющей собой почти идеальную прямую линию. Исходя из свойств логарифмов, нетрудно вывести, что исходная L-образная кривая представляет собой степенн у ю зависимость, которая описывается функцией вида

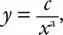
где x — население города, у — количество городов, имеющих такой размер, с — константа, а показатель степени a (показатель степенн о й зависимости) определяет отрицательный наклон прямой линии.

Степенн ы е распределения91 имеют некоторые нелогичные, с точки зрения традиционной статистики, свойства. Например, в отличие от нормального распределения, их моды, медианы и средние значения не совпадают из-за скошенной асимметричной формы L-образных кривых. Президент Буш извлек из этого немалую пользу, заявив в 2003 году, что сокращение налогов позволило каждой семье сэкономить в среднем 1586 долларов92. Хотя математически это верно, здесь он к своей выгоде взял за основу среднее значение вычета, под которым скрывались огромные вычеты в сотни тысяч долларов, полученные 0,1% богатейшего населения страны. Известно, что «хвост» в правой части распределения дохода следует степенн о й зависимости, и в подобной ситуации использование средней величины вводит в заблуждение, поскольку она далека от своего реального значения. В действительности большинству семей вернули менее 650 долларов. В данном распределении медиана значительно меньше, чем среднее значение.

Этот пример демонстрирует важнейшее свойство распределений степенн о й зависимости: они имеют «тяжелые хвосты» по сравнению по крайней мере с маленькими «жидкими хвостиками» нормального распределения. Подобные большие хвосты хотя и редкость, но встречаются чаще в распределениях данных, чем обычные колоколообразные кривые.

В «черный понедельник», 19 октября 1987 года, промышленный индекс Доу-Джонса упал на 22%. По сравнению с обычным уровнем нестабильности на фондовом рынке это падение составило более двадцати стандартных отклонений. Согласно традиционной статистике (в которой используется нормальное распределение), подобное событие практически невозможно: его вероятность составляет менее чем один случай на 100 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 (10 в 50 степени). Однако это произошло — поскольку колебания цен на фондовом рынке93 не соответствовали нормальному распределению. Для их описания лучше подходят распределения с «тяжелым хвостом».

Подобное происходит с землетрясениями, пожарами и наводнениями, что усложняет страховым компаниям задачу управления рисками. Такая же математическая модель описывает число погибших в результате войн и террористических атак, а также другие, гораздо более мирные вещи, такие как количество слов в романе или число сексуальных партнеров у человека.

Хотя прилагательные, используемые для описания длинных хвостов, выставляют их в не слишком выгодном свете, «хвостатые» распределения гордо несут свои хвосты. Жирный, тяжелый и длинный? Да, это так. Но в таком случае покажите, какой нормальный?

23. Шансы — это…

Вам когда-нибудь снился страшный сон, будто вам нужно сдать экзамен по предмету, который вы не изучали? Преподавателям обычно снятся «противоположные» сны: что они читают лекцию по дисциплине, о которой ничего не знают.

Такое случается со мной, когда я веду курс теории вероятностей94. Меня никогда ей не учили, и то, что мне приходится читать лекции по этому предмету, — страшно, смешно и очень похоже на дом с привидениями в парке развлечений.

Однако чаще всего мое сердце колотится, когда я сталкиваюсь с темой условной вероятности, то есть вероятности того, что некое событие А произойдет при условии, что произойдет некое событие B. Это скользкое понятие легко спутать с вероятностью наступления B при условии A. Однако это разные вещи, и нужно быть очень внимательным при вычислении их вероятностей. В качестве примера рассмотрим следующую задачу.

Прежде чем отправиться на недельный отдых, вы просите приятеля поливать ваши комнатные цветы, которые и так еле живы. Если их не поливать, то вероятность того, что они погибнут, составит 90%. Если поливать регулярно, то вероятность их гибели будет равна 20%. Вероятность того, что ваш друг забудет их полить, составляет 30%. Вопрос А: какова вероятность того, что ваши растения не погибнут за эту неделю? Вопрос В: если по возвращении вы обнаружите, что они засохли, какова вероятность того, что ваш друг забыл их полить? Вопрос С: если ваш друг забыл их полить, какова вероятность того, что они погибнут к вашему возвращению? Хотя вопросы В и С звучат похоже, они разные. В действительности в условии задачи уже содержится ответ на вопрос С — 90%. Однако как учесть все вероятности, чтобы получить ответы на вопросы В и А?95

Естественно, на протяжении нескольких первых семестров преподавания этой темы я засел за книги и стал делать медленные, но верные успехи. И постепенно начал кое-что замечать. Многие мои студенты не использовали теорему Байеса, которой я их обучал, а решали задачу равноценным способом, казавшимся им более простым.

Открытия, год за годом совершаемые изобретательными студентами, стали для меня лучшим способом размышления над условными вероятностями. В предложенных способах решения студенты прибегали к помощи интуиции, вместо того чтобы отвергать ее. Трюк состоял в том, чтобы мыслить натуральными числами, а не абстрактными категориями, такими как процентное соотношение, шансы или вероятности. Как только вы перестроите свое сознание, туман рассеется.