Стивен Строгац - Удовольствие от Х

18. Хоть ломтиками, хоть кубиками

66. Более подробную информацию о том, как интегральное исчисление помогает ученым, борющимся с раком, см. D. Mackenzie, Mathematical modeling of cancer, SIAM News, Vol. 37 (January/February 2004), и H. P. Greenspan, Models for the growth of a solid tumor by diffusion, Studies in Applied Mathematics (December 1972), pp. 317–340.

67. В математической литературе два одинаковых круглых цилиндра, оси которых пересекаются под прямым углом, называются по-разному: тело Штейнмеца, или бицилиндр. Для подготовленного читателя см. http://mathworld.wolfram.com/SteinmetzSolid.html и http://en.wikipedia.org/wiki/Steinmetz_solid. На страничке «Википедии» тоже есть очень полезная компьютерная анимация, которая показывает, как из пересекающихся цилиндров появляется призрачное тело Штейнмеца. Его объем современными методами можно рассчитать прямолинейно, но не прозрачно.

Архимед и Цзу Чунчжи знали более простое решение с использованием метода нарезки на кусочки и сравнения площадей квадрата и круга. Удивительно ясное изложение представлено в Martin Gardner’s column Mathematical games: Some puzzles based on checkerboards, Scientific American, Vol. 207 (November 1962), p. 164. Об Архимеде и Цу Чунчжи см. Archimedes, The Method, English translation by T. L. Heath (1912), reprinted by Dover (1953); и T. Kiang, An old Chinese way of finding the volume of a sphere, Mathematical Gazette, Vol. 56 (May 1972), pp. 88–91.

Мортон Мур отмечает, что бицилиндр также нашел применение в архитектуре: «Римляне и норманны при возведении цилиндрических сводов зданий были знакомы с геометрией пересекающихся цилиндров, где при пересечении двух таких сводов формировался крестообразный свод». Об этом и применении бицилиндров в кристаллографии см. M. Moore, Symmetrical intersections of right circular cylinders, Mathematical Gazette, Vol. 58 (October 1974), pp. 181–185.

68. Интерактивная демонстрация бицилиндров и других задач интегрального счисления доступна онлайн на The Wolfram Demonstrations Project (http://demonstrations.wolfram.com/). Чтобы с ними поиграть, нужно загрузить бесплатный интерактивный Mathematica Player (http://www.wolfram.com/products/player/), который в дальнейшем позволит вам исследовать сотни других интерактивных примеров из всех разделов математики. Наглядную демонстрацию бицилиндра см. на The bicylinder demo по адресу http://demonstrations.wolfram.com/IntersectingCylinders/.

Мамикон Мнацаканян на сайте Калифорнийского технологического института (Caltech) представил серию анимаций, иллюстрирующих Архимедов метод разбиения на кусочки и его мощь. Моя любимая страничка: http://www.its.caltech.edu/~mamikon/.

На Sphere.html изображены красивые отношения между объемами сферы и двойного конуса и цилиндра, чьи высота и радиус совпадают с радиусом сферы. Это же более наглядно можно увидеть, виртуально сливая воду из цилиндра в две другие формы, см. http://www.its.caltech.edu/~mamikon/SphereWater.html.

Такие же элегантные механические аргументы на службе у математики приведены в работе M. Levi, The Mathematical Mechanic (Princeton University Press, 2009).

69. Применение механического метода Архимеда к задаче нахождения объема бицилиндра см. T. L. Heath, ed., Proposition 15, The Method of Archimedes, Recently Discovered by Heiberg (Cosimo Classics, 2007), р. 48.

На странице 13 этого же тома Архимед признается, что рассматривает свой механический метод как средство для поиска теорем, а не их доказательства: «Некоторые вещи сначала мне стали ясны благодаря механическому методу, хотя в дальнейшем они должны были бы быть представлены средствами геометрии, потому что их исследование механическим методом фактически было просто демонстрацией. Но, конечно, найти доказательство проще, заранее получив некоторые знания по этому вопросу, чем если их не иметь».

Популярное изложение работы Архимеда см. R. Netz and W.Noel, The Archimedes Codex (Da Capo Press, 2009).

70. Фундаментальная теорема интегрального исчисления — теорема Ньютона–Лейбница. Далее цитата из «Википедии»: «Теорема Ньютона–Лейбница утверждает, что дифференцирование и интегрирование являются взаимно обратными операциями. Точнее, это касается значения первообразных для определенных интегралов. Поскольку, как правило, легче вычислить первообразную, чем применять формулу определенного интеграла, теорема дает практический способ вычисления определенных интегралов. Она также может быть интерпретирована как точное утверждение о том, что дифференцирование является обратной операцией интегрирования.

Теорема гласит: если функция f непрерывна на отрезке [ a , b ] и F есть функция, производная которой равна f на интервале ( a , b ), то:

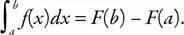
Кроме того, для любого x из интервала ( a , b )

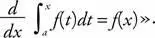
19. Все о числе e

71. Все ипостаси числа e и экспоненциальной функции представлены в книге E. Maor, e: The Story of a Number (Princeton University Press, 1994). Читатели, которые знакомы с интегральным исчислением, насладятся статьей B. J. McCartin, e: The master of all, Mathematical Intelligencer, Vol. 28, № 2 (2006), pp. 10–21. PDF-версия доступна по адресу http://mathdl.maa.org/images/upload_library/22/Chauvenet/mccartin.pdf.

72. «Упаковочный» коэффициент для пар, случайно рассаживающихся в кинотеатре, в научной литературе был изучен на других примерах. Он впервые возник в органической химии, см. P. J. Flory, Intramolecular reaction between neighboring substituents of vinyl polymers, Journal of the American Chemical Society, Vol. 61 (1939), pp. 1518–1521. Более современное изучение этого вопроса относится к проблеме случайной парковки, классическим головоломкам в теории вероятностей и статистической физике, см. W. H. Olson, A Markov chain model for the kinetics of reactant isolation, Journal of Applied Probability, Vol. 15, № 4 (1978), pp. 835–841.

73. Вопрос о том, когда прекращать перебирать партнеров и останавливать выбор на будущем супруге, изучался в различных формах и имеет различные названия: задача о невесте, задача о вступлении в брак, задача о капризном поклоннике, задача о выкупе султана за невесту. Но наиболее распространенное в настоящее время название — это задача секретаря. (Воображаемый сценарий найма лучшего секретаря из данного списка кандидатов. Вы беседуете с каждым претендентом по отдельности и должны решить, берете ли вы его на работу или прощаетесь навсегда). Для ознакомления с этой замечательной математической головоломкой и ее историей см. http://mathworld.wolfram.com/SultansDowryProblem.html и http://en.wikipedia.org/wiki/Secre­tary_problem. Для дополнительных сведений обратитесь к статье T. S. Ferguson, Who solved the secretary problem? Statistical Science, Vol. 4, № 3 (1989), pp. 282–289. Понятное изложение решения этой задачи можно найти по адресу http://www.math.uah.edu/stat/urn/Secretary.html. Для лучшего ознакомления с теорией оптимальных правил остановки см. T. P. Hill, Knowing when to stop: How to gamble if you must — the mathematics of optimal stopping, American Scientist, Vol. 97 (2009), pp. 126–133.

20. Любит не любит

74. Модели любовных отношений, основанные на дифференциальных уравнениях, см. S. H. Strogatz, Nonlinear Dynamics and Chaos (Perseus, 1994).

75. Анаграмму Ньютона см. V. I. Arnold, Geometrical Methods in the Theory of Ordinary Differential Equations (Springer, 1994).

76. Хаос в задаче о трех телах обсуждается в I. Peterson, Newton’s Clock (W.H. Freeman, 1993).

77. Цитату о том, как задача о трех телах вызывала головную боль у Ньютона, см. D. Brewster, Memoirs of the Life, Writings, and Discoveries of Sir Isaac Newton (Thomas Constable and Company, 1855), Vol. 2, p. 158.