Ричард Фейнман - 1. Современная наука о природе, законы механики

Прежде всего давайте рассмотрим несколько примеров слу­чайных блужданий. Их можно описать «чистым» продвижением D N за N шагов. На фиг. 6.5 показаны три примера путей при случайном блуждании.

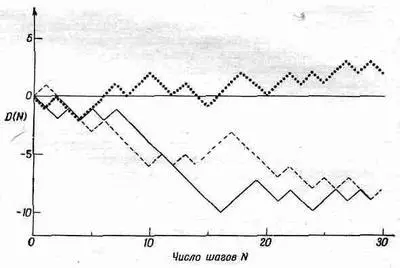
Фиг. 6.5. Три примера случайного блуждания.

По горизонтали отложено число шагов N, по вертикали — координата

D(N), т. е. чистое расстояние от начальной точки.

(При построении их в качестве случай­ной последовательности решений о том, куда сделать следующий шаг, использовались результаты подбрасывания монеты, при­веденные на фиг. 6.1.)

Что можно сказать о таком движении? Ну, во-первых, можно спросить: как далеко мы в среднем продвинемся? Нужно ожи­дать, что среднего продвижения вообще не будет, поскольку мы с равной вероятностью можем идти как вперед, так и назад. Однако чувствуется, что с увеличением N мы все с большей вероятно­стью можем блуждать где-то все дальше и дальше от начальной точки. Поэтому возникает вопрос: каково среднее абсолютное расстояние, т. е. каково среднее значение \D\? Впрочем, удобнее иметь дело не с |D|, а с D 2 ; эта величина положительна как для положительного, так и для отрицательного движения и поэтому тоже может служить разумной мерой таких случайных блу­жданий.

Можно показать, что ожидаемая величина D 2 N равна просто N — числу сделанных шагов. Кстати, под «ожидаемой величи­ной» мы понимаем наиболее вероятное значение (угаданное наилучшим образом), о котором можно думать как об ожидаемом среднем значении большого числа повторяющихся процессов

блуждания. Эта величина обозначается как 2 N> и называется, кроме того, «средним квадратом расстояния». После одного

шага D 2 всегда равно +1, поэтому, несомненно, 2 1 > = 1. (За единицу расстояния всюду будет выбираться один шаг, и поэтому я в дальнейшем не буду писать единиц длины).

, Ожидаемая величина D 2 N для N >1 может быть получена из d n -1 . Если после (N- 1) шагов мы оказались на расстоянии D N -1 , то еще один шаг даст либо D N =D N --1 +1, либо D N =D N -1 - 1. Или для квадратов

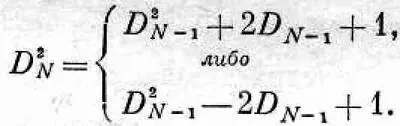
(6.7)

Если процесс повторяется большое число раз, то мы ожидаем, что каждая из этих возможностей осуществляется с вероятно­стью 舣/ 2, так что средняя ожидаемая величина будет просто средним арифметическим этих значений, т. е. ожидаемая вели­чина D 2 N будет просто D 2 N -1+1. Но какова величина D 2 N _ 1 , вер­нее, какого значения ее мы ожидаем? Просто, по определению, ясно, что это должно быть «среднее ожидаемое значение» 2 N -1>, так что

2 N>=2 N -1+1. (6.8)

Если теперь вспомнить, что 2 1>= 1, то получается очень простой результат:

N >=N. (6.9)

Отклонение от начального положения можно характеризо­вать величиной типа расстояния (а не квадрата рас­стояния); для этого нужно просто извлечь квадратный корень из <.D 2 N> и получить так называемое «среднее квадратичное рас­стояние» D C - K :

D C - K=Ц2> = ЦN. (6.10)

Мы уже говорили, что случайные блуждания очень похожи на опыт с подбрасыванием монет, с которого мы начали эту главу. Если представить себе, что каждое продвижение вперед или назад обусловливается выпадением «орла» или «решки», то D N будет просто равно N o -N P , т. е. разности числа выпа­дений «орла» и «решки». Или поскольку N o+N p=N(где N — полное число подбрасываний), то D N = 2N o- N. Вспомните, что раньше мы уже получали выражение для ожидаемого рас­пределения величины n o[она обозначалась тогда через k; см. уравнение (6.5)]. Ну а поскольку N — просто постоянная, то теперь такое же распределение получил ось и для D. (Выпаде­ние каждого «орла» означает невыпадение «решки», поэтому в связи между n oи Dпоявляется множитель 2.) Таким образом, на фиг. 6.2 график представляет одновременно и распределение расстояний, на которые мы можем уйти за 30 случайных шагов k=15 соответствует D = 0, a k = 16 соответствует D= 2 и т. д.).

Отклонение n oот ожидаемой величины N/2 будет равно

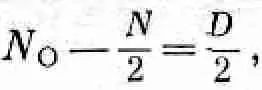
(6.11)

откуда для среднего квадратичного отклонения получаем

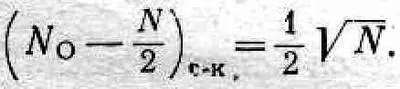
(6.12)

Вспомним теперь наш результат для d c - k . Мы ожидаем, что среднее расстояние, пройденное за 30 шагов, должно быть рав­но V30 = 5,5, откуда среднее отклонение k от 15 должно быть 5,5:2 = 2,8. Заметьте, что средняя полуширина нашей кривой на фиг. 6.2 (т. е. полуширина «колокола» где-то посредине) как раз приблизительно равна 3, что согласуется с этим результатом.

Теперь мы способны рассмотреть вопрос, которого избегали до сих пор. Как узнать, «честна» ли наша монета? Сейчас мы можем, по крайней мере частично, ответить на него. Если мо­нета «честная», то мы ожидаем, что в половине случаев выпадет «орел», т. е.

o>/N = 0,5. (6.13)

Одновременно ожидается, что действительное число выпадений «орла» должно отличаться от N/2на величину порядка ЦN/2, или, если говорить о доле отклонения, она равна

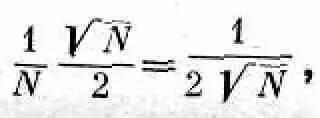
т. е. чем больше N, тем ближе к половине отношение N o /N.

На фиг. 6.6 отложены числа N O /N для тех подбрасываний монеты, о которых мы говорили раньше.

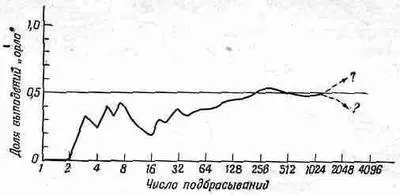
Фиг. 6.6. Доля выпадений «орла» в некоторой частной последовательности N подбрасываний монеты.

Как видите, при уве­личении числа N кривая все ближе и ближе подходит к 0,5. Но, к сожалению, нет никаких гарантий, что для каждой дан­ной серии или комбинации серий наблюдаемое отклонение будет близко к ожидаемому отклонению. Всегда есть конечная веро­ятность, что произойдет большая флуктуация — появление большого числа выпадений «орла» или «решки»,— которая даст произвольно большое отклонение. Единственное, что можно сказать,— это если отклонения близки к ожидаемому 1/ 2ЦN (скажем, со множителем 2 или 3), то нет оснований считать монету «поддельной» (или что партнер плутует).