Алекс Беллос - Красота в квадрате
- Название:Красота в квадрате
- Автор:
- Жанр:
- Издательство:Манн, Иванов и Фербер
- Год:2015
- ISBN:9785000576052
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Алекс Беллос - Красота в квадрате краткое содержание
Красота в квадрате - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Если говорить языком математики, частота встречаемости слов в романе «Улисс» приближенно подчиняется следующему закону:
частота × ранг = 26 500
Эту формулу можно привести к такому виду:
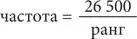
В общем виде данное уравнение выглядит так:
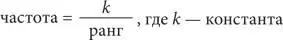
Следовательно, частотность употребления того или иного слова обратно пропорциональна его рангу (порядковому номеру) в списке, упорядоченном по убыванию частоты. Другими словами, если ранг слова в n раз больше, то частота его использования в n раз меньше.
Изучив другие тексты, Ципф пришел к выводу, что во всех книгах на всех языках частота встречаемости слов и их порядковый номер в частотном списке находятся в обратной зависимости, но с небольшим уточнением:
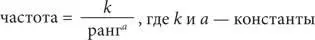
Это уравнение известно как закон Ципфа. (Когда два числа записаны в форме x y , мы говорим « x в степени y », и это значит, что число x умножается само на себя y раз. Как мы знаем со школьных лет, 4 2= 4 × 4, а 2 3= 2 × 2 × 2. Однако число y может быть не только целым числом. Следовательно, 2 1,5означает, что число 2 умножается само на себя 1,5 раза, а это равно 2,83. Чем ближе значение числа y к 1, тем ближе x y к числу x .)
Ципф обнаружил, что значение константы a всегда стремится к 1 независимо от того, кто автор книги и каково ее содержание. То есть зависимость между частотой встречаемости слов и их рангом всегда очень близка к обратно пропорциональной зависимости. В случае романа «Улисс» значение a равно 1.
Я считаю закон Ципфа чрезвычайно увлекательным. Он раскрывает заманчиво простую математическую закономерность, определяющую выбор слов. Я решил выяснить, соблюдается ли этот закон в книге, которую вы сейчас читаете. Для подсчета частотности слов я воспользовался компьютерной программой, а не гуммированной бумагой и ножницами. Просматривая частотную таблицу, я увидел, что частота встречаемости слов действительно обратно пропорциональна их порядковому номеру в таблице. Самое распространенное слово, употребляемое мною в книге («the»), встречается в десять раз чаще, чем десятое по частоте слово «was», примерно в сто раз чаще, чем сотое по частоте слово «who», и в тысячу раз чаще, чем тысячное слово «spirals».
Когда я составил на основе данных о частоте и ранге слов график (первый график, представленный ниже), оказалось, что соответствующие точки лежат близко к координатным осям. График, отображающий обратно пропорциональную зависимость, всегда представляет собой L-образную кривую. Сначала кривая резко снижается, а затем быстро выравнивается и переходит в своего рода «длинный хвост». Это говорит о том, что одни слова встречаются в тексте в огромном количестве, а другие почти не используются. (На самом деле во всех текстах, независимо от их объема, около 50 процентов слов употребляются только один раз. В данной книге таких слов 51 процент [8].)
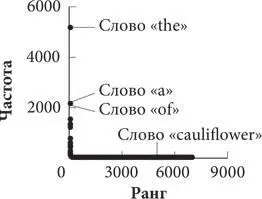
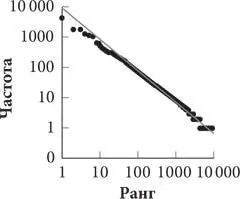
Распределение частотности слов в книге «Алекс в Зазеркалье»
На нижнем графике отображены те же данные, но изменен масштаб. Расстояние от 1 до 10, от 10 до 100 и от 100 до 1000 теперь одинаковое на обеих осях, другими словами, мы имеем двойной логарифмический масштаб. График, напоминающий провисший кабель, как по волшебству превратился в туго натянутую струну. Появился некий математический порядок: точки графика образуют почти идеальную прямую.
Прямая линия на графике, построенном в двойном логарифмическом масштабе, — доказательство того, что эти данные подчиняются закону Ципфа (в Приложении 2 я объясню почему). С математической точки зрения прямая линия более полезна, чем кривая с длинным хвостом, поскольку ее свойства легче анализировать. В частности, у прямой есть постоянный градиент. Мы вернемся к понятию градиента немного позже, а пока вам нужно знать только то, что градиент — это степень наклона: отношение расстояния, покрытого прямой по вертикали, к расстоянию по горизонтали. Если нарисовать линию наилучшего соответствия и определить ее градиент, он и будет представлять собой константу a в уравнении закона Ципфа. Я рассчитал градиент линии на расположенном выше графике. Он чуть больше единицы, а это значит, что по сравнению с Джеймсом Джойсом я чаще использую самые распространенные слова и реже — наименее распространенные.
При более близком рассмотрении не все точки на графике попадают на прямую линию. Некоторые отклоняются от нее, особенно примерно двадцать слов, встречающихся в тексте чаще всего. Однако в большинстве случаев точки находятся очень близко к этой линии. Поразительно то, что порядковый номер подавляющего количества слов в этой книге позволяет достаточно точно определить частоту их использования, и наоборот.
Профессор Ципф обнаружил такую же обратно пропорциональную зависимость еще в одной книге — книге переписи населения США 1940 года. Однако в этот раз он подсчитывал не частотность слов, а численность населения крупных американских городов.
Муниципальный район
Ранг
Население
Нью-Йорк / северо-восток Нью-Джерси
1
12 миллионов
Кливленд
10
1,2 миллиона
Гамильтон/Мидлтаун
100
0,11 миллиона
В это трудно поверить, но и здесь прослеживается та же закономерность. В Нью-Йорке (самом крупном городе США) численность населения в десять раз больше, чем в Кливленде (десятом по величине городе), и в сто раз больше, чем в Гамильтоне (сотом по величине городе). Никто не предлагал американцам расселяться с такой точностью. Тем не менее их выбор подчинялся строгой закономерности. Это происходит и сейчас. На самом деле все мы поступаем именно так. На представленных ниже графиках в двойном логарифмическом масштабе отображены данные о численности населения американских городов и их ранге (порядковом номере), взятые из отчетов о переписи населения США 2000 года, а также данные о численности населения крупнейших городов мира.
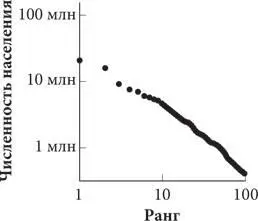
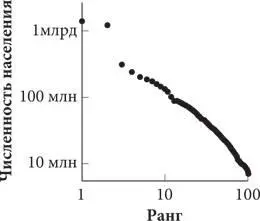
Интервал:
Закладка:









