Алекс Беллос - Красота в квадрате

Уравнение степенной зависимости между объемом и площадью обозначается также термином «закон масштабирования», поскольку оно демонстрирует, что происходит с измеримой величиной объекта (в данном случае площадью поперечного сечения) в результате увеличения общего размера.

В 30-х годах ХХ столетия швейцарский зоолог Макс Клайбер измерил вес нескольких видов млекопитающих и их уровень метаболизма (минимальное количество энергии, вырабатываемое животными в состоянии покоя) [18]. Когда ученый отобразил полученные данные на графике в двойном логарифмическом масштабе, получилась прямая линия, на основании которой он вывел следующий степенной закон:

скорость обмена веществ ≈ 70 (масса) ¾

Этот закон известен как закон Клайбера. Впоследствии биологи расширили его действие на всех теплокровных животных, как показано на представленном ниже рисунке. Скорость обмена веществ растет не так быстро, как масса, а это говорит о том, что чем крупнее животные, тем эффективнее они вырабатывают энергию. Было также выявлено, что жизнь животных подчиняется и многим другим законам масштабирования. Например, продолжительность жизни животных прямо пропорциональна массе в степени ¼, а частота сердечных сокращений обратно пропорциональна массе в степени ¼. Поскольку коэффициент степенного закона — это в большинстве случаев величина, кратная ¼, биологические степенные законы называют законами четвертного степенного масштабирования. Учитывая разнообразие животного мира (размер млекопитающих колеблется от этрусской мыши весом около одного грамма до голубого кита, который в 100 миллионов раз тяжелее), действительно замечательно, что информация о размере животного позволяет так много сказать о нем.

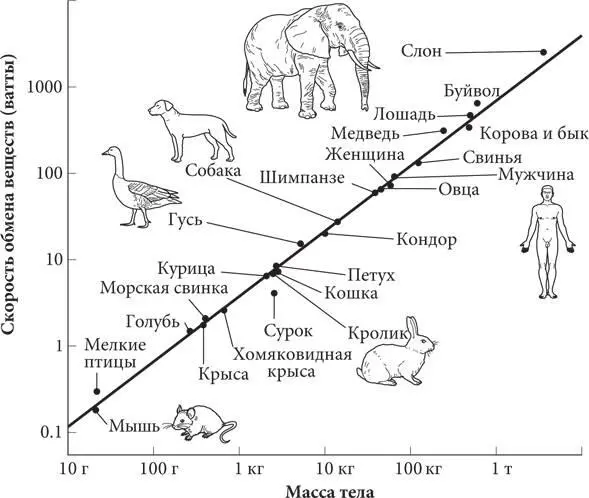
Закон Клайбера

Физик Джеффри Уэст из Института Санта-Фе и биологи Джеймс Браун и Брайан Энквист из Университета Нью-Мексико разработали математическую теорию, которая объясняет эффект четвертного степенного масштабирования [19]. Если в общих чертах, то они утверждают, что при рассмотрении любого организма как транспортной системы (кровь поступает в аорту, разветвляющуюся на артерии, которые, в свою очередь, разветвляются на более узкие кровеносные сосуды) ее оптимизация под имеющееся пространство порождает степенной закон. Подробное объяснение данного феномена выходит за рамки материала этой книги, но представляет интерес в данном контексте в связи с другой работой Уэста — изучением организма иного типа: города.

Уэст и его коллеги обнаружили, что масштабирование по степенному закону весьма характерно для маленьких и больших городов [20]. Проанализировав огромное количество экономических и социальных данных и отобразив полученные результаты на графиках в двойном логарифмическом масштабе, они установили, что в США имеют место следующие закономерности:

количество изобретателей = k (численность населения) 1,25

совокупная заработная плата = k (численность населения) 1,12

количество случаев заболевания СПИДом = k (численность населения) 1,23

количество тяжких преступлений = k (численность населения) 1,16

В этих уравнениях показатель степени (экспонента) больше 1, а это значит, что чем крупнее город, тем в нем больше изобретателей, совокупной заработной платы, случаев заболеваний СПИДом и тяжких преступлений на душу населения. Здесь налицо пропорциональная зависимость. По всем этим городским индикаторам значение показателей степени составляет примерно 1,2, и такая сосредоточенность вокруг одного значения интересна сама по себе. Исходя из этого, получается, что при увеличении размера города вдвое можно ожидать роста количества изобретателей, совокупной заработной платы, случаев заболеваний СПИДом и тяжких преступлений на душу населения на 15 процентов.

В случае ряда других городских индикаторов показатель степени меньше 1, а это значит, что рост города может привести к сокращению следующих показателей на душу населения:

количество автозаправочных станций = k (численность населения) 0,77

длина электрических кабелей = k (численность населения) 0,83

При увеличении размера города в два раза количество автозаправочных станций и длина электрических кабелей на душу населения могут сократиться на 15 процентов. Другими словами, в городах имеет место математически прогнозируемая экономия от масштаба — и это происходит во всем мире. «Японские города развивались абсолютно независимо от европейских и американских городов, тем не менее закон масштабирования действует [в каждой стране], — говорит Уэст. — Это наводит на мысль о существовании некой универсальной движущей силы». Уэст убежден, что степенные законы действуют в городах по той же причине, что и в мире животных. Город — это и транспортная сеть. Подобно тому как кровеносная система обеспечивает перемещение крови по толстым, а затем по все более тонким сосудам, города тоже распределяют ресурсы по сети разветвляющихся дорог, кабелей и труб.

Мы сами решаем, где нам жить, на что тратить деньги и как расходовать свое время. Тем не менее, если взглянуть на наше коллективное поведение сквозь призму чисел, становится очевидным, что оно вполне предсказуемо и подчиняется простым, взаимно совместимым математическим законам. Мы так распределены по земному шару, что в 30 процентах больших и малых городов численность населения начинается с единицы, размер городов в целом обратно пропорционален их номеру в упорядоченном по численности населения списке и все города являются версиями друг друга, образованными по принципу степенного масштабирования. Возможно, в чем-то этот мир сложен. Но в чем-то — достаточно прост.

Числа — незаменимый инструмент, помогающий нам понять мир, в котором мы живем. То же самое можно сказать о фигурах. Именно изучение одной из фигур дало начало развитию западной математики.

3. Любовные треугольники

Роб Вудолл — коллекционер геодезических знаков. В этом он преуспел как никто другой. Геодезические знаки представляют собой бетонные сооружения высотой до пояса, которыми обозначаются базисные точки национальной геодезической сети, использовавшейся в свое время картографами и топографами. Если вы когда-либо бывали в сельских районах Великобритании, то наверняка видели эти сооружения. Они, как правило, расположены на вершинах холмов — как трофей в конце восхождения. За период с 1936 по 1962 год Управление геодезии и картографии установило более 6500 таких знаков, 6200 из них сохранились до настоящего времени. По посещению, или «коллекционированию», геодезических знаков проводятся соревнования. На счету 50-летнего Роба Вудолла уже 6155 знаков — другими словами, почти все [1]. На данный момент он опережает ближайшего соперника почти на тысячу знаков.