Алекс Беллос - Красота в квадрате

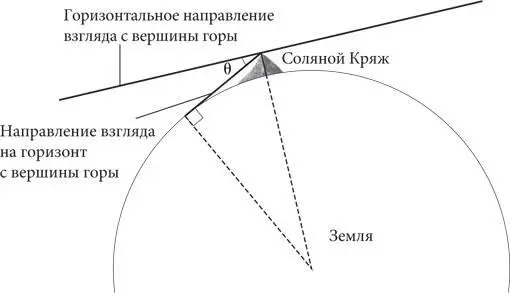
Измерение радиуса Земли по методу аль-Бируни

Соотношение сторон треугольника стало настоящим открытием для архитекторов, астрономов, артиллеристов, ученых и мореплавателей. К тому же это послужило толчком к формированию абстрактной математики, позволяющей по-новому взглянуть на классические геометрические концепции, такие как теорема Пифагора, которая гласит, что:

a 2+ b 2= c 2,

где c — гипотенуза, a и b — два катета.

Если α — это угол между сторонами b и c , тогда:

Другими словами, a = c sin α, а b = c cos α. Мы можем подставить эти значения в уравнение Пифагора:

( c sin α) 2+ (c cos α) 2= c 2,

которое можно преобразовать так:

c 2(sin α) 2+ c 2(cos α) 2= c 2

и привести к следующему виду:

(sin α) 2+ (cos α) 2= 1

Прекрасно! Теперь у нас есть компактная формула, демонстрирующая, как можно вычислить синус по косинусу и наоборот без необходимости рисовать треугольник. Это простейшее из уравнений, которые называют тригонометрическими тождествами — уравнениями, включающими в себя тригонометрические функции. Принято считать, что арабский математик ибн-Юнус (современник аль-Бируни) вывел следующую формулу:

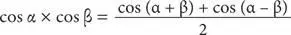
Она имела огромное значение, хотя математикам понадобилось пять сотен лет, чтобы понять почему. Уравнение ибн-Юнуса позволяет заменить такую трудную математическую операцию, как умножение, на более простое действие — сложение.

Представьте, что нам нужно умножить 0,2897 на 0,3165.

Оба числа находятся в диапазоне от 0 до 1, стало быть, есть такие углы, для которых эти числа являются косинусами. Определить, какие именно углы соответствуют данным значениям, помогут тригонометрические таблицы. Вот эти углы:

cos 73,160° = 0,2897

cos 71,548° = 0,3165

Следовательно, мы можем записать уравнение так:

0,2897 × 0,3165 = cos 73,160° × cos 71,548°

Приведенное выше тождество говорит о том, что эта формула эквивалентна следующему уравнению:

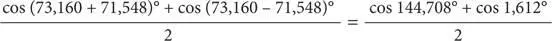
Обратившись к таблицам, получим тождество:

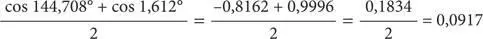
Это и есть результат умножения чисел 0,2897 и 0,3165, причем очень точный. Умножьте их с помощью калькулятора, округлите произведение до четвертого десятичного знака, и получите 0,0917.

Приведенный выше способ умножения чисел может показаться слишком сложным, но в конце XVI столетия он был самым легким. Вместо того чтобы расписывать операцию умножения в столбик, что требует больших усилий и времени, достаточно просто посмотреть в сборник тригонометрических таблиц, сложить два числа, найти их разность, снова посмотреть в таблицы, сложить два числа и разделить их на два. Этот метод обозначается термином простаферез ис (prosthaphaeresis), который образован от греческих слов, означающих сложение и вычитание, — prosthesis и aphaeresis .

Метод простаферезиса вдохновил шотландца Джона Непера на поиск еще более эффективного способа преобразования умножения в сложение, что в 1614 году привело к открытию логарифма. Вместо умножения двух чисел теперь можно было сложить их логарифмы. Логарифмы Непера существенно упростили процесс умножения, из-за чего метод простаферезиса утратил популярность. Тем не менее на протяжении нескольких десятилетий триумфа прямоугольный треугольник — квинтэссенция геометрии — играл двойную роль в качестве невидимого оружия арифметики.

Хотя треугольники, несомненно, весьма полезны по отдельности, в командной игре они особенно эффективны. Если нарисовать сеть треугольников (как показано на рисунке ниже) и измерить в ней все углы, то достаточно определить точную длину одной линии, чтобы рассчитать длину всех остальных линий сети. Предположим, нам известна точная длина линии, выделенной жирным; обозначим ее как l . Тригонометрическое тождество, которое принято называть теоремой синусов, дает нам формулу расчета длины двух других сторон треугольника:

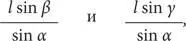
где α — угол, противоположный жирной линии, β и γ — два других угла треугольника. Поскольку все углы в треугольниках сети известны, на основании длины каждой очередной линии можно вычислить длину двух других линий — и так далее, пока не будет известна длина каждой линии сети. Этот метод применим к любым треугольникам, а не только к прямоугольным.

В 1533 году голландский математик Гемма Фризиус понял, что метод триангуляции как нельзя лучше подходит для картографии, поскольку измерять углы гораздо легче, чем большие расстояния [10]. Его идея состояла в том, чтобы выбрать точки на местности так, чтобы от каждой из них было видно две других, и построить таким образом сеть треугольников. Он измерил углы между точками с помощью теодолита — круглого транспортира на подставке. Определив длину базисной линии, Гемма Фризиус смог рассчитать все остальные расстояния, используя тригонометрические таблицы, а затем нарисовал точную карту местности.

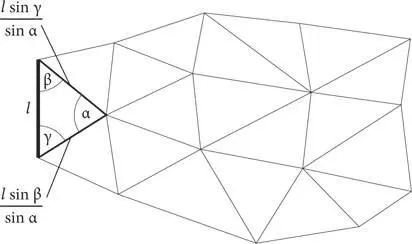
Триангуляция

Франция стала первой страной, в которой триангуляция была выполнена по всей территории, и произошло это в 1668 году. Единственная сложная задача в любом виде триангуляции заключается в измерении первого расстояния. Аббат Жан Пикар взял за основу участок прямой дороги от Вильжюиф до Жувиньи длиной в 11 километров, который тщательно измерил с помощью деревянных мерных реек. Затем Пикар отправился на север, используя в качестве вершин треугольников такие ориентиры, как часовые башни и вершины холмов, и измеряя только углы между ними. Добравшись до Атлантического океана, Пикар обнаружил, что побережье гораздо ближе расположено к Парижу, чем считалось раньше. «Твоя работа стоила мне приличной части моих владений!» — фыркнул Людовик XIV. Начатый Пикаром процесс триангуляции продолжался еще столетие после его смерти, пока территорию Франции не покрыли четыре сотни треугольников. Знаменитая карта Франции, составленная в итоге, содержала больше деталей, чем любая другая из созданных ранее карт, и была выполнена почти в том же масштабе, что и стандартные туристические карты Michelin, доступные в наше время.