Алекс Беллос - Красота в квадрате

Чуть позже Галилей поддразнил Кеплера еще одной анаграммой, но на этот раз она имела смысл и носила намеренно провокативный характер: «Haec immatura a me iam frustra leguntur — oy» , или «Этa ущербность рaзбирaется мною покa безуспешно». В данном случае Кеплер тоже нашел решение со смыслом: «Macula rufa in Jove est gyratur mathem etc» — «Ибо Юпитер, увы, говорят, вертится, испачканный красным пятном». На самом деле Галилей хотел передать такое послание: «Cynthiae figuras aemulatur Mater Amorum» — «Мать любви [Венера] подражает фигурам Цинтии [Луны]» (это означало, что у Венеры тоже есть фазы, напоминающие фазы Луны). Тем не менее ошибочный перевод Кеплера снова оказался пророческим. Через пятьдесят лет астрономы увидели, что у Юпитера действительно есть красное пятно — гигантский атмосферный вихрь, известный как Большое красное пятно.

Галилей и Кеплер изменили представление об ученых, превратившись из пассивных исследователей в героев-первооткрывателей. Имея перед собой единственную Вселенную, каждый из них хотел получить признание как человек, определивший ее строение. После Галилея многие ученые, в том числе Роберт Хук, Христиан Гюйгенс и Исаак Ньютон, использовали не поддающиеся расшифровке анаграммы, для того чтобы защитить свою интеллектуальную собственность. Так продолжалось до тех пор, пока публикация в журнале не стала в XVIII столетии стандартным способом объявить о последних научных достижениях.

Галилей принял теорию Коперника о том, что Земля вращается вокруг Солнца, но опровергал гипотезу Кеплера об эллиптической форме орбит планет [10]. Несмотря на это, Галилей добился серьезных успехов в изучении движения сферических объектов другого типа. Летом 1592 года в качестве молодого профессора математики он посетил своего друга и покровителя, маркиза Гвидобальдо дель Монте в его замке в Урбино. Маркиз был назначен генеральным инспектором укреплений Тосканского герцогства, а это означало, что для него особый интерес представляла траектория движения пушечных ядер. Они летят по прямой линии, а затем падают вниз, как предполагала традиционная аристотелевская механика, или двигаются по какой-то кривой, прежде чем долетят до цели?

Для того чтобы выяснить это, друзья провели эксперимент, который оказался настолько простым, что трудно было поверить, как никто не додумался до этого раньше. Они взяли два небольших металлических шара, окунули их в чернила и запустили по диагонали по наклонной плоскости. След, оставленный каждым из шаров, представлял собой симметричную дугу. Галилей видел, что шары поднимаются вверх точно так же, как и опускаются вниз: траектория движения вверх представляет собой зеркальное отображение траектории падения. Эта симметрия навела Галилея на мысль о том, что движение можно разделить на горизонтальные и вертикальные элементы. В свободном полете характер движения объекта по горизонтали отличается от характера вертикального движения. Впоследствии Галилей провел и другие эксперименты с шарами, покрытыми чернилами, продемонстрировав, что если тело брошено со стола горизонтально, то:

1)-горизонтальное смещение пропорционально затраченному времени. Так, если тело проходит 1 единицу расстояния за 1 секунду, оно пройдет 2 единицы за 2 секунды, 3 единицы за 3 секунды и т. д.;

2)-вертикальное смещение пропорционально квадрату затраченного времени. Так, если тело падает на 1 единицу расстояния за 1 секунду, оно упадет на 4 единицы за 2 секунды, на 9 единиц за 3 секунды и т. д.

На основании знаний о свойствах конических сечений, открытых Аполлонием, Галилей смог сделать вывод, что траектория движения шара, запущенного со стола, представляет собой параболу, как показано на рисунке слева [11]. Когда какое-либо тело, например баскетбольный мяч, запускается под углом (рисунок справа), оно тоже движется по параболе, но сначала мяч должен подняться по одной ее стороне, а затем опуститься по другой ее стороне. Такая парабола является траекторией движения объекта, свободно движущегося под воздействием силы тяжести. Это может быть струя фонтана, полет стрелы или движение мяча, брошенного в воздух. Писатель Томас Пинчон назвал свой выдающийся роман Gravity’s Rainbow16 в соответствии с описанием оставленного немецкой ракетой «Фау-2» параболического следа, представляющего собой метафору расцвета и падения культур.

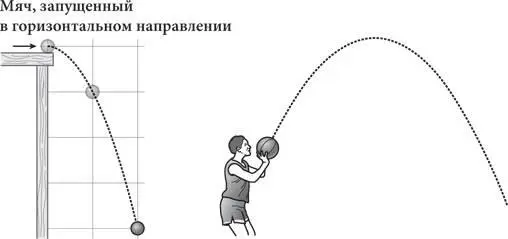
На протяжении почти двух тысяч лет конические сечения считались вершиной древнегреческой математической мысли, красивыми кривыми без какой-либо практической функции. Затем были открыты сразу две области их применения, которые, как оказалось, «скрывались» у всех на виду: планеты перемещаются по эллиптическим орбитам, а брошенные тела — по параболам. В конце XVII века Исаак Ньютон продемонстрировал, как оба эти следствия вытекают из его законов движения и всемирного тяготения. Галилей и Кеплер изучали одну и ту же проблему в разных масштабах. (Строго говоря, брошенный в воздух камень на самом деле начинает двигаться по эллиптической орбите вокруг Земли, и он бы завершил процесс, если бы масса Земли была сосредоточена в ее центре. Однако, с точки зрения наблюдателя, мы можем предположить, что брошенный камень движется по параболе.)

У парабол есть одно важное, удивительное свойство: все они имеют одну и ту же форму. Как параболу ни уменьшай или ни увеличивай, она останется подобной другим параболам, точно так же как окружность не меняет своей формы при изменении диаметра. Это вытекает из нашего первоначального определения конических сечений, согласно которому каждый угол наклона секущей плоскости образует уникальную фигуру. Окружность и парабола могут быть образованы только под одним углом: в случае окружности секущая поверхность должна быть параллельной основанию конуса, а в случае параболы — боковой поверхности конуса. Эллипс и гипербола могут быть получены под разными углами наклона секущей поверхности, а значит, они могут иметь разную форму.

Для описания параболы существуют два определения: 1) это геометрическое место точек, равноудаленных от заданной точки и заданной линии, известных как фокус и директриса (см. рисунок 1); и 2) это кривая, которая, будучи сделанной из отражающего материала, отражает все лучи света, исходящего из фокуса, параллельно друг другу (см. рисунок 2).

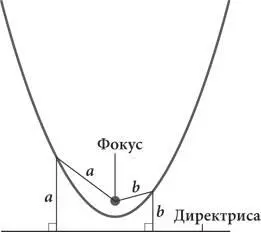
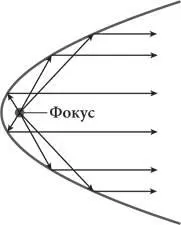
Геометрия параболы