Алекс Беллос - Красота в квадрате

Первое определение предоставляет оригамистам легкий способ построения параболы. Обозначьте точку F на листе бумаги, как продемонстрировано на первом рисунке ниже. Возьмите произвольную точку P на нижней кромке листа и сложите лист так, чтобы совместить эти точки друг с другом, как показано стрелкой. Полученную линию сгиба отметьте пунктиром. Повторите данную процедуру для множества точек, расположенных на нижней кромке листа бумаги. Полученная в итоге кривая — это парабола. (Подсказка: каждый сгиб образует линию, точки которой равноудалены от фокуса и произвольной точки.)

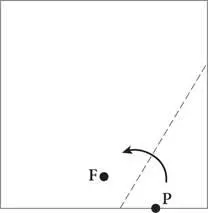
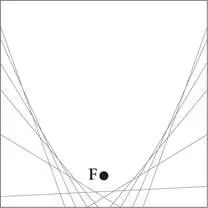
Построение параболы посредством сгибания листа бумаги

Второе определение объясняет, почему парабола — самая распространенная кривая в магазине осветительных приборов. Если лампочка установлена в фокусе параболического зеркала, лучи света отражаются параллельно. Вращение параболы вокруг ее центральной оси образует параболоид, в форме которого и сделаны отражающие зеркала в фонариках, прожекторах и автомобильных фарах.

Этот процесс работает и в обратном направлении. Параллельные лучи света, поступающие в параболоид, отражаются его поверхностью в фокус. Следовательно, если задача рефлектора — собрать в пучок солнечные лучи (которые можно считать параллельными, поскольку Солнце находится очень далеко), понадобится параболическая поверхность. Параболоиды широко применяются в технологии использования солнечной энергии. Например, отражатель Шеффлера, параболическая металлическая чаша, повсеместно используется в развивающихся странах для приготовления пищи. Он направлен на Солнце и медленно поворачивается вслед за его движением, для того чтобы поймать как можно больше солнечных лучей, отражая их в одну и ту же точку (фокус), в которой находится плита. Самая мощная солнечная печь представляет собой параболическое зеркало высотой 45 метров, расположенное во французских Пиренеях, неподалеку от Одейо. Из-за огромных размеров само зеркало не двигается, а принимает отраженный солнечный свет от 63 маленьких плоских вращающихся зеркал. В фокусе зеркала находится круглый щит, который в солнечные дни нагревается до 3500 °С — достаточно высокая температура, для того чтобы варить свинец, плавить вольфрам или превратить дикого кабана в пепел.

Солнечная печь в Одейо, Франция

© Иэн Фрейзер/Shutterstock.com

Параболические антенны служат также для приема электромагнитных и звуковых волн, поступающих в фокус от удаленных объектов. Такие антенны уже стали привычным элементом городского пейзажа: чаще всего они устанавливаются на крышах домов тех людей, которые смотрят спутниковое телевидение, но их можно встретить и на командно-диспетчерских пунктах и военных объектах. Шпионы, инженеры звукозаписи на телевидении и орнитологи используют параболические микрофоны для улавливания тихих звуков с большого расстояния. Принцип во всех случаях один и тот же. Параболоид — единственная геометрическая фигура, отражающая параллельные волны в определенную точку.

В 1668 году Исаак Ньютон построил первый «отражающий» телескоп, ключевыми элементами которого были зеркала, а не линзы, использовавшиеся в телескопах до этого. Ньютон понял, что для основного зеркала самая оптимальная форма — параболоид, но не смог изготовить такое зеркало, поэтому ему пришлось довольствоваться сферическим. Однако даже при наличии подобного дефекта отражающий телескоп был гораздо лучше, чем предыдущие модели, поэтому, начиная с XVII века, большинство телескопов были зеркальными.

Кроме того, Ньютон сделал в отношении парабол одно открытие, которое представляло в то время сугубо теоретический интерес, а сейчас успешно применяется в промышленном производстве телескопов. Если вращать цилиндрический сосуд, наполненный жидкостью, ее поверхность принимает форму параболоида. Под воздействием вращения жидкость поднимается выше у стенок сосуда и образует углубление в центре, создавая поперечное сечение в форме параболы. На этом свойстве построен один из способов изготовления параболических зеркал — вращать сосуд с расплавленным стеклом и дать этому стеклу застыть в таком положении. Большой бинокулярный телескоп, один из самых мощных телескопов в мире, был сделан именно так. Телескоп состоит из двух параболических зеркал диаметром 8,4 метра, изготовленных в огромной вращающейся печи в подземной лаборатории, расположенной под футбольным полем Аризонского университета в Тусоне. Хотя лаборатория может выпускать в год всего по одному зеркалу ценой в десятки миллионов долларов, это все равно более дешевый и быстрый метод, чем изготовление аналогичного зеркала посредством шлифовки стекла.

Еще дешевле телескоп с жидким зеркалом — в нем используется вращающийся цилиндр, наполненный отражающей жидкостью. Большой зенитный телескоп возле Ванкувера представляет собой чашу, наполненную ртутью, которая во время вращения принимает форму параболоида. На настоящий момент это самый дешевый из крупных телескопов мира, но у него есть один серьезный недостаток: чаша вращается в горизонтальной плоскости, а значит, телескоп может быть направлен только прямо вверх, в зенит.

В 1637 году французский математик Рене Декарт изобрел систему координат, что стало самым значительным прорывом в понимании конических сечений со времен Аполлония. Декартова система координат определяет положение точки на плоскости по ее расстоянию от вертикальной и горизонтальной оси [12]. Каждая точка имеет уникальные координаты ( a, b ), где a — это позиция на горизонтальной оси, а b — на вертикальной (см. рисунок 1 ниже). Данная система позволяла математикам описывать кривые посредством уравнений и представлять уравнения в виде кривых. Следовательно, она создала мост между геометрией, изучающей фигуры, и алгеброй, изучающей уравнения, которые были до этого разными математическими дисциплинами.

По сложившейся традиции мы записываем уравнения с помощью переменных x и y , отображающих позицию на горизонтальной и вертикальной оси, другими словами — координаты ( x, y ). Например, график уравнения x = y представляет собой совокупность всех точек с координатами ( x, y ), где x = y . Как показано на рисунке 2, это точки с координатами (1, 1), (2, 2), (3, 3) и т. д. С другой стороны, график уравнения y = x 2 — это совокупность всех точек, у которых y = x 2. Это точки с координатами (0, 0), (1, 1), (2, 4), (3, 9) и т. д. Такая кривая, представленная на рисунке 3, представляет собой параболу, касающуюся горизонтальной оси в начале системы координат или в точке с координатами (0, 0). Но, поскольку школьная программа больше ориентирована на алгебру, чем на геометрию, наша первая встреча с параболой происходит в момент построения графика уравнения y = x 2. Возможно, вы узнаете ее как старого друга, первую U-образную кривую, которая встретилась вам в процессе изучения элементарной математики.