Алекс Беллос - Красота в квадрате

[12]Joao Gama Oliveira and Albert-Laszlo Barabasi, Human dynamics: Darwin and Einstein correspondence patterns, Nature, 2005.

[13]Takashi Iba et al., Power-Law Distribution in Japanese Book Sales Market, Fourth Joint Japan-North America Mathematical Sociology Conference, 2008.

[14]Mark Buchanan, Ubiquity, Weidenfeld & Nicolson, 2000.

[15]Albert-Laszlo Barabasi, Linked, Perseus, 2002; Albert-Laszlo Barabasi, Bursts, Penguin, 2010.

[16]Michael P. H. Stumpf and Mason A. Porter, Critical Truths About Power Laws, Science, 2012; Aaron Clauset, Cosma Rohilla Shalizi, and M. E. J. Newman, Power-Law Distributions in Empirical Data, SIAM Review, 2009.

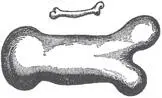
[17]В книге Discourses and Mathematical Demonstrations Relating to Two New Sciences («Беседы и математические доказательства двух новых наук») Галилей сделал следующий набросок двух костей — маленькой и тонкой, а также большой и толстой. Он писал, что у большого животного большая кость «выполняла бы ту же функцию, что и маленькая кость у маленького животного».

Компания по выпуску игрушек для собак Nylabone продает нейлоновые жевательные кости, имеющие точно такую же форму, как на представленном ниже рисунке. В компании утверждают, что эти кости (получившие название Galileo) — «самые прочные жевательные кости для собак».

[18]Melanie Mitchell, Complexity: A Guided Tour, Oxford University Press, 2009.

[19]Geoffrey B. West, James H. Brown, and Brian J. Enquist, A General Model for the Origin of Allometric Scaling Laws in Biology, Science, 1997.

[20]Luis M. A. Bettencourt et al., Growth, innovation, scaling, and the pace of life in cities, PNAS, 2007.

ГЛАВА 3

[1]Роб посетил 6177 геодезических знаков, расположенных в Великобритании, в том числе 45 полуразрушенных и 100 опрокинутых. Большинство геодезических столбов, которые Роб еще не видел, находятся на островах. Он издали видел два геодезических знака, размещенных на земле Министерства обороны, в том числе знак, установленный на территории базы обслуживания атомных подводных лодок в Кулпорте (Шотландия). Однако Робу не разрешили приблизиться к ним. Еще только четыре коллекционера смогли пройти 3000 геодезических знаков.

[2]Практические аспекты предложенного Фалесом метода измерения высоты пирамид рассматриваются в статье: Thales’ Shadow’ by Lothar Redlin, Ngo Viet and Saleem Watson, in Mathematics Magazine, 2000. В частности, авторы демонстрируют, что солнечные лучи направлены перпендикулярно грани пирамиды два раза в день только весной и летом: один раз утром и один раз вечером.

[3]Не исключено, что египтяне обладали гораздо более обширными знаниями в области математики, чем принято считать, но установить это невозможно, поскольку об этом сохранилось слишком мало информации.

[4]Carl B. Boyer, A History of Mathematics, John Wiley & Sons, 1968.

[5]В прошлом «две другие стороны» обозначались термином catheti (единственное число — cathetus), но в настоящее время в английском языке этот термин вышел из употребления. Однако в других языках он используется до сих пор: Kathete — в немецком языке, cateto — в испанском и португальском, катеты — в русском языке.

[6]Florian Cajori, A History of Mathematical Notations, Dover, 1993.

[7]Georges Ifrah, The Universal History of Numbers, John Wiley & Sons, 2000.

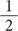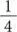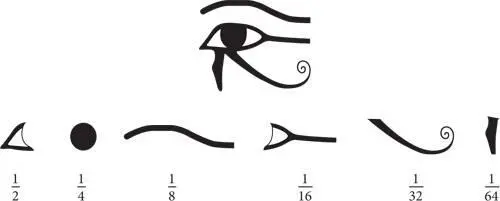
[8]Самая гибкая система с использованием единичных дробей — бинарная система, в которой дроби образуются так: половина, половина половины, половина половины половины и т. д., или , , , 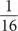… В этой системе любая дробь может быть записана в виде комбинации единичных дробей. В 1911 году египтолог Георг Мюллер написал, что в ходе исследований открыл невероятно живописное древнее изображение первых шести единичных дробей бинарной системы. На представленном ниже рисунке изображен символ «око Гора», каждый элемент которого соответствует одной из этих дробей: левая часть роговицы — 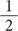, зрачок — 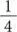, бровь — и т. 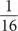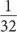д.; остальные фрагменты представляют дроби , и 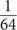. Шестьдесят три возможные комбинации фрагментов «ока Гора», отличных от нуля, позволяют выразить любую дробь от 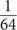до 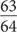. Помимо волнующего изображения «око Гора» имеет и не менее волнующую историю: это мистический символ Гора — бога с головой сокола, глаз которого был разделен на шесть частей его дядей и впоследствии снова собран воедино. К сожалению, после целого столетия принятия в 2002 году миф о глазе Гора был развенчан Джимом Риттером, который заявил об отсутствии каких бы то ни было доказательств того, что фрагменты «ока Гора» символизируют единичные дроби. Jim Ritter, Closing the Eye of Horus: the Rise and Fall of Horus-Eye Fractions, Under One Sky: Astronomy and Mathematics in the ancient Near East, 2002.

[9]В полном виде греческая система обозначения чисел выглядела так:

α

β

γ

δ

ε

ς

ζ

η

q

1

2

3

4

5

6

7

8

9

ι

κ

λ

μ

ν

ξ

ο

π

ϙ

10

20

30

40

50

60

70

80

90

ρ

σ

τ

υ

ϕ

χ

ψ

ω

ϡ

100

200

300

400

500

600

700

800

900

[10]Eli Maor, Trigonometric Delights, Princeton University Press, 1998.

[11]John Keay, The Great Arc, HarperCollins, 2000.

ГЛАВА 4

[1]При условии, что шар не начнет вращаться.

[2]www.lds.org/locations/temple-square-salt-lake-city-tabernacle.

[3]Carl B. Boyer, A History of Mathematics, John Wiley & Sons, 1968.

[4]Помимо сугубо математического, слово «парабола» имеет и другое значение, поскольку древнегреческое слово parabola означает не только «бросить рядом»28, но и «сравнить». В литературе парабола — это простой короткий рассказ иносказательного характера, в котором присутствует сравнение с более сложным сюжетом. От этого значения происходит французское слово parler («разговаривать») и многие английские слова, от parliament («парламент») до parole («пароль»).

[5]Arthur Koestler, The Sleepwalkers, Hutchinson, 1959.

[6]Математическое объяснение того, почему циклы и эпициклы позволяют описать любую замкнутую непрерывную орбиту, основано на двух концепциях, о которых я часто упоминаю в этой книге: комплексные числа и ряды Фурье. Подобно тому как волну можно разложить на синусоиды, путь в комплексной плоскости можно разложить на ряд круговых вращений.

[7]Santiago Ginnobili and Christian C. Carman, Deferentes, Epiciclos y Adaptaciones, Filosofia e historia da ciencia no Cone Sul, 2008.

[8]Arthur Koestler, The Sleepwalkers, Hutchinson, 1959.

[9]Norwood Russell Hanson, Patterns of Discovery, CUP, 1961. Хэнсон начинал в качестве трубача, а во время Второй мировой войны стал летчиком-истребителем. Получив прозвище Летающий Профессор, он продолжал летать в мирное время и прославился выполнением фигур высшего пилотажа. Хэнсон погиб в возрасте 42 лет, когда его самолет разбился в штате Нью-Йорк из-за густого тумана.