Алекс Беллос - Красота в квадрате

h = ( d + e ) tan α

h = e tan β

Следовательно:

( d + e ) tan α = e tan β

Что можно записать в таком виде:

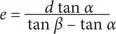
Исходя из равенства h = e tan β , мы можем утверждать, что:

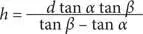
В этом уравнении высота рассчитывается только с использованием значений α, β и d .

РАДИУС ЗЕМЛИ

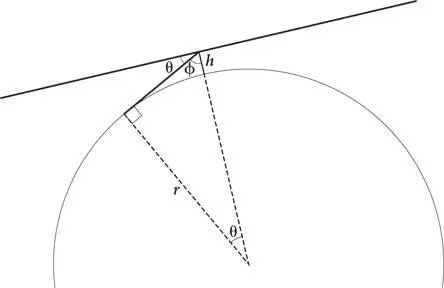
На этом рисунке представлен тот же треугольник, что и на соответствующем рисунке в главе 3. Нам известен угол между горизонталью и горизонтом θ и высота горы h . Наша задача — вычислить радиус Земли r .

Сначала надо показать, что угол, исходящий из центра Земли, равен θ. На рисунке видно, что угол ϕ равен 90º – θ. Поскольку сумма углов в треугольнике составляет 180º, то искомый угол равен θ.

Мы знаем, что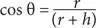

Следовательно:

( r + h ) cos θ = r

r cos θ + h cos θ = r

Эти равенства можно преобразовать так:

r – r cos θ = h cos θ

r (1 – cos θ) = h cos θ

Тогда

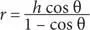
Приложение 4

МАШИНА УМНОЖЕНИЯ

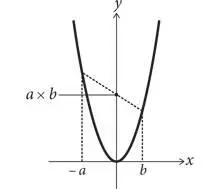
Утверждение.Для того чтобы умножить a × b , необходимо построить на параболе y = x 2прямую из точки x = − а до точки x = b , как показано на рисунке. Прямая линия, соединяющая эти две точки, пересекает ось y в точке a × b .

Доказательство.Примем за истинное следующее утверждение: уравнение прямой, проходящей через точку с координатами ( p , q ), имеет вид y – q = ( x – p ) m , где m — градиент.

Прямая на графике проходит через точки с координатами (− a , a 2) и ( b , b 2).

Градиент этой прямой, который представляет собой отношение расстояния по вертикали к расстоянию по горизонтали, рассчитывается по формуле 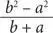, которую можно преобразовать к виду 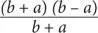, затем это вы­ражение можно сократить до ( b – a ).

Следовательно, уравнение прямой выглядит так:

y – a 2= ( x + a ) ( b – a )

Его можно преобразовать следующим образом:

y – a 2= xb – xa + ab – a 2

Члены – a 2можно сократить, после чего останется такое уравнение:

y = xb – xa + ab

Если прямая пересекает вертикальную ось, тогда x = 0, а значит,

y = ab

Другими словами, прямая пересекает ось в точке ab , что равно a × b .

Приложение 5

Если сумма S наращивается со скоростью r , то после t периодов начисления сложных процентов значение этой суммы равно

S (1 + r ) t

Сумма удвоится, когда (1 + r ) t = 2. Чтобы решить это уравнение, необходимо взять натуральный логарифм обеих его частей. Натуральный логарифм — это логарифм с основанием е , который обозначается как ln. Таким образом

ln (1 + r ) t = ln 2

Что сводится к

t ln (1 + r ) = ln 2

Следовательно,

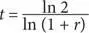
Когда r имеет небольшое значение, то ln (1 + r ) ≈ r , стало быть, это уравнение можно записать так:

Что эквивалентно

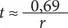
Если r — скорость, выраженная в дробном виде, то обозначим через R скорость в процентном выражении. В таком случае необходимо умножить числитель и знаменатель в дроби t на 100

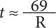
Следовательно, количество периодов начисления сложных процентов t , необходимых для удвоения суммы, составляет 69 разделить на темпы роста в процентах R.

Поскольку число 72 легче делится на другие числа, чем 69, в правиле 72 чаще всего используется именно это число, хотя значение 69 было бы точнее27.

Приложение 6

Площадь самого большого заштрихованного квадрата составляет 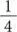. Второй по величине заштрихованный квадрат имеет площадь, равную четверти самого большого квадрата, то есть 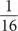. Площадь третьего по величине квадрата составляет четверть этой площади и т. д. Следовательно, общая площадь заштрихованных квадратов равна

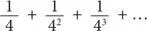
Однако каждому заштрихованному квадрату соответствует ровно по два незаштрихованных квадрата одинакового размера. Таким образом, площадь заштрихованных квадратов должна также составлять 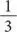общей площади. Стало быть,

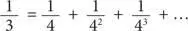
Приложение 7

КАК СПРАВЕДЛИВО РАЗДЕЛИТЬ ПИРОГ НА ТРОИХ

Назовем этих троих Гуго, Стефан и Станислав — по именам математиков, внесших самый большой вклад в создание «Шотландской книги».

Шаг 1.Гуго делает первый разрез. Его задача — отрезать 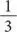пирога.

Шаг 2.Гуго передает свой кусок Стефану, который должен оценить, равен ли он 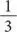пирога или нет. Если, по его мнению, кусок слишком большой, он отрезает от него немного.

Шаг 3.Кусок передается Станиславу, который решает, брать его или нет. Если Станислав берет кусок, Гуго и Стефану предстоит разделить оставшийся большой кусок, а также небольшой кусочек, отрезанный Стефаном. Один из них делит оба куска надвое, а другой выбирает.

Шаг 4.Если Станислав не берет кусок пирога, существуют две возможности в зависимости от того, обрезал ли Стефан кусок Гуго.

Если Стефан обрезал кусок, он должен его взять. Двое других делят оставшийся кусок пирога, как в шаге 3.

Если Стефан не обрезал кусок, тогда его берет Гуго, а двое других делят остаток.

С точки зрения логики это правильный подход, но в случае его применения на практике можно запутаться.