Алекс Беллос - Красота в квадрате

Теорема (theotrem):утверждение, которое не является самоочевидным, но доказано методом дедукции.

Теория множеств (set theory):раздел математики, который изучает свойства множеств и их способность стать основой для арифметики.

Триангуляция (triangulation):измерение расстояний с помощью тригонометрических функций.

Тригонометрия (trigonometry):раздел математики, изучающий тригонометрические функции и их использование.

Факториал (factorial):факториал целого числа — это произведение всех целых чисел от 1 до этого числа включительно. Например, факториал числа 5, который записывается как 5!, равен 5 × 4 × 3 × 2 × 1 = 120.

Фокус (focus):основная точка, которая используется при построении конических сечений.

Форма (shape):внешняя геометрическая конфигурация объекта, не зависящая от его размера и положения в пространстве.

Фрактал (fractal):объект, который обладает свойством самоподобия.

Хорда (chord):отрезок, соединяющий две точки окружности.

Числовая ось (number line):геометрическая интерпретация чисел, расположенных по порядку на непрерывной прямой, простирающейся до минус бесконечности слева и до плюс бесконечности справа от ноля, находящегося посредине.

Целое число (whole number):в контексте данной книги — любое положительное число 1, 2, 3…

Циклоида (cycloid):траектория движения точки, находящейся на ободе колеса, которое перемещается по прямой.

Экспонента (exponent):см. показатель степени .

Экспоненциальный рост/спад (exponential growth/decay):возрастание или убывание величины, при котором скорость роста (спада) пропорциональна значению самой величины.

Эксцентриситет (eccentricity):степень отклонения конического сечения от окружности.

Приложение 1

Логарифм можно определить следующим образом.

Если a = 10 b , то логарифм числа a равен b и записывается в таком виде26:

log а = b

Другими словами, если число а выражено в виде степени 10, то логарифм числа а — это показатель степени. Вот некоторые простые значения логарифмов:

log 10 = 1, поскольку 10 = 10 1

log 100 = 2, поскольку 100 = 10 2

log 1000 = 3, поскольку 1000 = 10 3

А вот таблица логарифмов чисел от 1 до 10:

log 1 = 0

log 2 = 0,301

log 3 = 0,477

log 4 = 0,602

log 5 = 0,699

log 6 = 0,778

log 7 = 0,845

log 8 = 0,903

log 9 = 0,954

log 10 = 1

Если мы отметим логарифмы чисел от 1 до 10 на числовой оси, разместив их в соответствии с их значениями, то получим логарифмическую шкалу от 0 до 1. Чем дальше по оси находятся логарифмы, тем плотнее они расположены.

На этой шкале я также отметил расстояние между логарифмами. Вы узнаете в них проценты из закона Бенфорда. Иными словами, если я случайным образом выберу на этой шкале точку от 0 до 1, вероятность того, что она попадет в интервал от log 1 до log 2, составляет 30,1 процента, в интервал от log 2 до log 3 — 17,6 процента и т. д.

Точно так же длина первого интервала равна log 2 – log 1, второго log 3 – log 2, а интервала d — log ( d + 1) – log d . Это означает, что эти вероятности можно более точно выразить как log ( d + 1) – log d для каждого значения d .

Приложение 2

Здесь я покажу вам, что в двойном логарифмическом масштабе любое уравнение вида 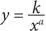всегда представлено прямой линией с наклоном влево, и наоборот: в двойном логарифмическом масштабе прямую с наклоном влево всегда можно описать представленным выше уравнением. Если на координатных осях откладываются логарифмы ранга и частотности, то прямая с наклоном влево отображает закон Ципфа:

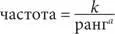
Для того чтобы понять изложенные ниже разъяснения, мы должны иметь определенное представление о координатной геометрии (о концепции градиента, например), а также об основных свойствах логарифмов. Кроме того, нам необходимо принять как истинное следующее утверждение.

(1) На координатной плоскости, где горизонтальная и вертикальная оси обозначаются как х и у , все прямые линии могут быть описаны уравнением y = mx + c , где m — это градиент прямой, а с — точка, в которой эта прямая пересекает вертикальную ось.

Итак, начнем с уравнения:

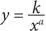
Возьмем логарифм от обеих его частей:

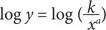
Согласно свойствам логарифмов, мы можем записать это уравнение в таком виде:

log y = log k – log x a

Или так:

log y = log k – a log x

Если log y = Y, а log x = X, то это уравнение можно записать следующим образом:

Y= – a X + log k

Исходя из представленного выше предположения (1), мы знаем, что на координатной плоскости, где Х — это горизонтальная ось, а Y — вертикальная, это прямая с градиентом – а , пересекающая вертикальную ось в точке log k .

Поскольку Х = log x , а Y = log y , этот график отображен в двойном логарифмическом масштабе, а так как градиент отрицательный, можно сделать вывод, что прямая должна быть наклонена влево.

Аналогичным образом представьте себе прямую с уклоном влево в двойном логарифмическом масштабе. Согласно предположению (1), ее можно описать таким уравнением:

log y = –log x + c

(Поскольку прямая наклонена влево, можно сказать, что она имеет отрицательный градиент.)

Если c = log k , это дает уравнение:

log y = – a log x + log k

или

log y = log k – a log x

Воспользовавшись свойствами логарифма, это уравнение можно преобразовать так:

log y = log k – log x a

Или так:

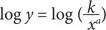
Что означает следующее:

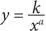
Что и требовалось доказать.

Дополнительный вывод состоит в том, что уравнение y = kx a описывает прямую с уклоном вправо в логарифмическом масштабе, а любая такая прямая может быть представлена данным уравнением.

Приложение 3

ВЫСОТА ГОРЫ

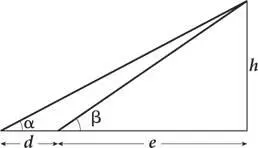
На рисунке изображены треугольники из главы 3. Наша задача — вычислить высоту горы h , зная только значения α, β и d . Пусть е — это расстояние от точки, находящейся непосредственно под вершиной, до ближайшей точки наблюдения.

Нам известно, что 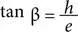, а также что 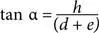. Преобразуем эти уравнения так: