Чарльз Уилан - Голая статистика

В зависимостях такого рода интересно то, что не каждое наблюдение вписывается в соответствующую схему. Иногда низкорослые люди весят больше, чем высокие. Иногда те, кто вообще не занимается спортом, бывают гораздо стройнее, чем те, кто регулярно выполняет физические упражнения. Тем не менее существует отчетливо выраженная связь между ростом и весом человека, а также между весом и физическими нагрузками.

Если построить диаграмму разброса данных, отражающих рост и вес произвольной выборки взрослых американцев, то получится примерно такая картина:

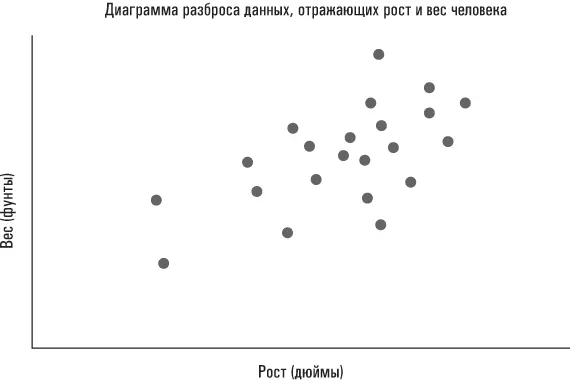
Если бы нам нужно было построить диаграмму разброса для данных о выполнении физических упражнений (количество минут, затрачиваемых на них каждую неделю) и данных о весе человека, то можно было бы ожидать отрицательной корреляции, причем те, кто занимается спортом больше времени, будут весить меньше. Однако картина в виде совокупности точек, разбросанных по определенной площади, представляет собой несколько неуклюжий инструмент. (Если бы Netflix попыталась предлагать мне какие-то фильмы, продемонстрировав диаграмму разброса рейтингов для тысяч кинолент, выставленных миллионами кинозрителей, то я посчитал бы такую рекомендацию просто неудачной шуткой.) Эффективность корреляции как статистического инструмента заключается в том, что мы можем выразить связь между двумя переменными с помощью одной описательной статистики – коэффициента корреляции.

Коэффициент корреляции обладает двумя чрезвычайно привлекательными характеристиками. Во-первых, в силу причин математического характера, которые мы обсудим в приложении, он представляет собой число в диапазоне от −1 до 1. Корреляция, равная 1 (иногда ее называют идеальной корреляцией), означает, что каждому изменению одной переменной соответствует эквивалентное изменение другой переменной в том же направлении.

Корреляция, равная –1 (иногда ее называют идеальной отрицательной корреляцией), означает, что каждому изменению одной переменной соответствует эквивалентное изменение другой переменной в противоположном направлении.

Чем ближе корреляция к 1 или –1, тем сильнее связь между переменными. Нулевая (или близкая к 0) корреляция говорит об отсутствии значимой связи между двумя переменными (например между результатом экзамена по математике и размером обуви экзаменуемого).

Второй привлекательной особенностью коэффициента корреляции является то, что с ним не связаны никакие единицы измерения. Мы можем рассчитать корреляцию между ростом и весом, несмотря на то что рост измеряется в дюймах, а вес – в фунтах. Мы можем даже вычислить корреляцию между количеством телевизоров, имеющихся дома у учеников, и результатами их экзаменов по математике (я почему-то уверен, что она окажется положительной). (Несколько ниже я остановлюсь подробнее на данной связи.) Коэффициент корреляции буквально творит чудеса: он сжимает сложное сочетание данных, измеряемых в разных единицах (наподобие наших диаграмм разброса роста и веса), в единственную элегантную описательную статистику.

Как это удается?

Как обычно, я привожу самую распространенную формулу для определения коэффициента корреляции в приложении, находящемся в конце этой главы. Это не та статистика, которую можно вычислить вручную. (После того как вы введете соответствующие данные, базовый программный пакет, например Microsoft Excel, рассчитает корреляцию между двумя соответствующими переменными.) Тем не менее на интуитивном уровне понять эту формулу несложно. Формула для вычисления коэффициента корреляции выполняет следующие операции:

1. Вычисляет среднее значение и стандатное (среднеквадратическое) отклонение для обеих переменных. Если вернуться к примеру с ростом и весом, то мы бы узнали средний рост людей в выборке, средний вес людей в той же выборке и стандартное отклонение для роста и веса.

2. Преобразует все данные таким образом, чтобы каждое наблюдение было представлено его расстоянием (в стандартных отклонениях) от среднего значения. Верьте мне, это совсем не сложно. Допустим, средний рост в выборке равняется 66 дюймам (при стандартном отклонении в 5 дюймов), а средний вес – 177 фунтов (при стандартном отклонении в 10 фунтов). Теперь предположим, что ваш рост – 72 дюйма, а вес – 168 фунтов. Мы можем также сказать, что ваш рост составляет 1,2 стандартного отклонения сверх среднего роста [(72 ‒ 66)/5) = 1,2] и 0,9 стандартного отклонения ниже среднего веса, или –0,9 применительно к нашей формуле [(168 ‒ 177)/10 = –0,9]. Да, это нетипично, когда рост человека выше среднего, а вес – ниже среднего, но поскольку вы уже заплатили неплохие деньги за эту книгу, то, как мне кажется, я должен в знак благодарности сделать вас высоким худощавым человеком . Обратите внимание: ваш рост и вес, выражавшиеся поначалу в дюймах и фунтах, теперь выражаются абстрактными числами 1,2 и – 0,9. Как видите, потребность в единицах измерения отпала.

3. Теперь я могу скрестить руки на груди и предоставить возможность компьютеру выполнить остальную работу. Формула вычисляет связь по всей выборке между ростом и весом, которые измеряются в стандартных единицах. Когда рост отдельных людей в выборке равняется, к примеру, 1,5 или 2 стандартного отклонения выше среднего значения, какими должны быть значения их веса, измеренные в стандартных отклонениях от среднего значения для веса? А когда рост членов выборки близок к среднему значению, какими будут значения их веса, измеренные в стандартных единицах?

Если расстояние от среднего значения для одной переменной в целом соответствует – по величине и направлению – расстоянию от среднего значения для другой переменной (например, для людей, рост которых существенно отличается в ту или другую сторону от среднего значения роста, значения их веса, как правило, существенно отличаются от среднего значения веса, причем в том же направлении, что и рост), то у нас есть основания говорить о сильной положительной корреляции.

Если же расстояние от среднего значения для одной переменной в целом соответствует аналогичному расстоянию от среднего значения для другой переменной, но в противоположном направлении (например, у людей, которые чаще среднего занимаются физическими упражнениями, как правило, вес гораздо ниже среднего), то у нас есть основания говорить о сильной отрицательной корреляции.

Если две переменные в целом не отклоняются от среднего значения сколь-нибудь существенно (например, размер обуви и интенсивность занятий физическими упражнениями), то мы можем говорить о незначительной или нулевой корреляции.