Нихиль Будума - Основы глубокого обучения

Фундаментальные идеи в области нейросетей существуют уже десятилетия, но лишь в последнее время основанные на них модели обучения стали популярными. Наш интерес к нейросетям во многом вызван их выразительностью, которая обеспечивается многослойностью. Как мы уже говорили, глубокие нейросети способны решать проблемы, к которым раньше было невозможно даже подступиться.

Однако полное их обучение сопряжено с разными сложностями, которые требуют множества технологических инноваций, в том числе больших размеченных массивов данных (ImageNet, CIFAR и т. д.), более передового «железа» с ускорителями GPU, а также новинок в области алгоритмов.

Многие годы исследователи прибегали к поуровневому «жадному» предварительному обучению для обработки сложных поверхностей ошибок в моделях глубокого обучения [41]. Эти стратегии требовали больших затрат времени и были направлены на поиск более точных вариантов инициализации параметров модели по слою за раз перед тем, как использовать мини-пакетный градиентный спуск для поиска оптимальных параметров. Но недавние прорывы в методах оптимизации позволяют нам непосредственно обучать модели от начала и до конца. В этой главе речь пойдет именно о них.

Несколько следующих разделов будут в основном посвящены локальным минимумам и тому, как они препятствуют успешному обучению глубоких моделей. Далее мы поговорим о невыпуклых поверхностях ошибок, порожденных глубокими моделями, о том, почему обычный мини-пакетный градиентный спуск часто недостаточен и как современные невыпуклые оптимизаторы преодолевают эти трудности.

Основные трудности при оптимизации моделей глубокого обучения связаны с тем, что мы вынуждены использовать информацию о локальных минимумах для выводов о глобальной структуре поверхности ошибок. Это серьезная проблема, ведь между локальной и глобальной структурами обычно мало связи. Рассмотрим такую аналогию.

Представьте себе, что вы — муравей, живущий в континентальной части США. Вас выбросили где-то в случайном месте, и ваша задача — найти самую низкую точку на этой поверхности. Как это сделать? Если вы можете видеть только то, что вас непосредственно окружает, задача кажется неразрешимой. Если бы поверхность США имела форму миски (была бы, говоря математически, выпуклой) и мы смогли бы удачно установить темп обучения, можно было бы воспользоваться алгоритмом градиентного спуска и в конце концов добраться до дна. Но рельеф США очень сложный. И даже если мы найдем какую-то долину (локальный минимум), мы не узнаем, действительно ли это самая низкая точка на карте (глобальный минимум). В главе 2 мы говорили о том, как мини-пакетный градиентный спуск помогает в продвижении по сложной поверхности ошибок, на которой есть проблемные районы с нулевым градиентом. Но, как видно из рис. 4.1, даже стохастическая поверхность ошибок не спасает от глубокого локального минимума.

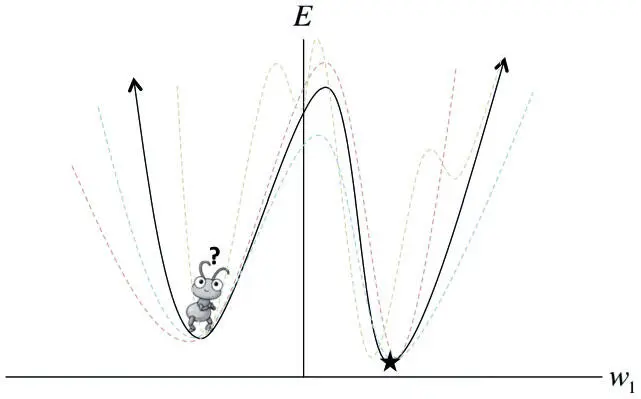
Рис. 4.1. Мини-пакетный градиентный спуск помогает избежать мелкого локального минимума, но редко эффективен при наличии глубокого локального минимума

И тут встает важный вопрос. Теоретически локальные минимумы — серьезная проблема. Но как часто они встречаются на поверхности ошибок глубоких сетей на практике? И при каких сценариях они действительно затрудняют обучение? В двух следующих разделах мы рассмотрим распространенные заблуждения относительно локальных минимумов.

Первый источник локальных минимумов связан с определимостью модели . Поверхности ошибок глубоких нейросетей гарантированно имеют значительное — иногда бесконечное — число локальных минимумов. И вот почему.

Внутри слоя полносвязной нейросети с прямым распространением сигнала любая перестановка нейронов не изменит данные на выходе. Проиллюстрируем это при помощи простого слоя из трех нейронов на рис. 4.2. Оказывается, что в слое из n нейронов существует n ! способов перестановки параметров. А для глубокой сети с l слоев, каждый из которых состоит из n нейронов, имеется n! l эквивалентных конфигураций.

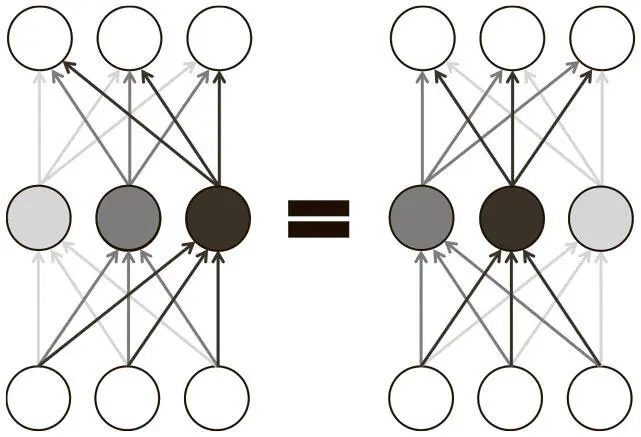
Рис. 4.2. Перестройка нейронов в слое нейросети приводит к эквивалентным конфигурациям в силу симметрии

Помимо симметрии перестроек нейронов, неопределимость присутствует в некоторых видах нейросетей и в других формах. Например, существует бесконечное число эквивалентных конфигураций, которые приводят к эквивалентным сетям для отдельного нейрона ReLU. Поскольку он использует кусочно-линейную функцию, мы можем умножить все веса входов на любую не равную 0 константу k , при этом умножая все веса выходов на 1/ k без изменения поведения сети.

Пусть активные читатели сами обоснуют это утверждение. В целом локальные минимумы из-за неопределимости глубоких нейросетей по природе своей не создают проблем. Ведь все неопределимые конфигурации ведут себя примерно одинаково независимо от того, какие входные значения в них поступают. Они дадут одну ошибку на обучающем, проверочном и тестовом наборах данных. Все они достигнут одинаковых успехов на обучающих данных и будут вести себя идентично при обобщении до неизвестных примеров.

Локальные минимумы становятся проблемой, только если они сомнительные . Тогда они соответствуют конфигурации весов в нейросети, которая вызывает ошибку больше, чем конфигурация в глобальном минимуме. Если локальные минимумы встречаются часто, мы вскоре столкнемся с серьезными проблемами при использовании градиентных методов оптимизации, поскольку учитывать можем только локальную структуру.

Много лет специалисты во всех проблемах при обучении глубоких сетей винили сомнительные локальные минимумы, даже не имея достаточных доказательств. Сейчас открытым остается вопрос, действительно ли такие минимумы с высокой частотой ошибок по сравнению с глобальными часто встречаются в реальных глубоких сетях. Однако, судя по последним исследованиям, у большинства локальных минимумов частота ошибок и характеристики обобщения не очень отличаются от глобальных минимумов.

Можно попробовать решить эту проблему наивным путем: построить график функции потерь во время обучения глубокой нейросети. Но эта стратегия не даст достаточно информации о поверхности ошибок, ведь трудно судить о том, действительно ли она так «ухабиста» или мы никак не можем понять, куда двигаться.