Нихиль Будума - Основы глубокого обучения

with tf.device(‘/gpu:2'):

a = tf.constant([1.0, 2.0, 3.0, 4.0], shape=[2, 2], name='a')

b = tf.constant([1.0, 2.0], shape=[2, 1], name='b')

c = tf.matmul(a, b)

sess = tf.Session(config=tf.ConfigProto(allow_soft_placement=True, log_device_placement=True))

sess.run(c)

TensorFlow также позволяет строить модели, которые используют несколько GPU. Они создаются в виде башни, как показано на рис. 3.3.

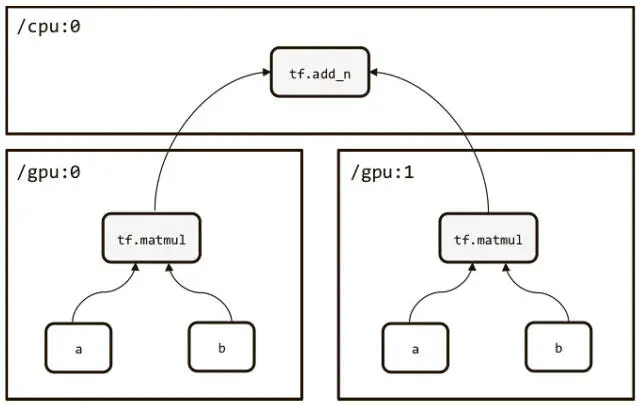
Рис. 3.3. Создание моделей для нескольких GPU в виде башни

Ниже приведен пример кода для нескольких GPU:

c = []

for d in [‘/gpu:0', ‘/gpu:1']:

with tf.device(d):

a = tf.constant([1.0, 2.0, 3.0, 4.0], shape=[2, 2], name='a')

b = tf.constant([1.0, 2.0], shape=[2, 1], name='b')

c. append(tf.matmul(a, b))

with tf.device(‘/cpu:0'):

sum = tf.add_n(c)

sess = tf.Session(config=tf.ConfigProto(log_device_placement=True))

sess.run(sum)

Мы рассмотрели базовые понятия TensorFlow и можем построить простую модель для набора данных MNIST. Как вы, наверное, помните, наша цель — распознать рукописные цифры по черно-белым изображениям 28×28 единиц. Первая сеть, которую мы построим, реализует простой алгоритм машинного обучения — логистическую регрессию [33].

Логистическая регрессия — метод, с помощью которого мы можем вычислить вероятность того, что входные данные относятся к одному из целевых классов. Определим вероятность того, что данное изображение — 0, 1… или 9.

Наша модель использует матрицу W , которая представляет веса соединений в сети, и вектор b , соответствующий смещению, для вычисления того, принадлежит ли входящее значение x классу i , при помощи функции мягкого максимума (softmax), о которой мы уже говорили выше:

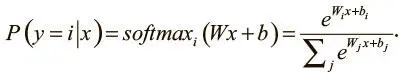
Наша задача — определить значения W и b , которые будут наиболее эффективно и точно классифицировать входящие данные. Сеть логистической регрессии можно выразить в схеме (рис. 3.4). Для простоты мы опустили смещения и их соединения.

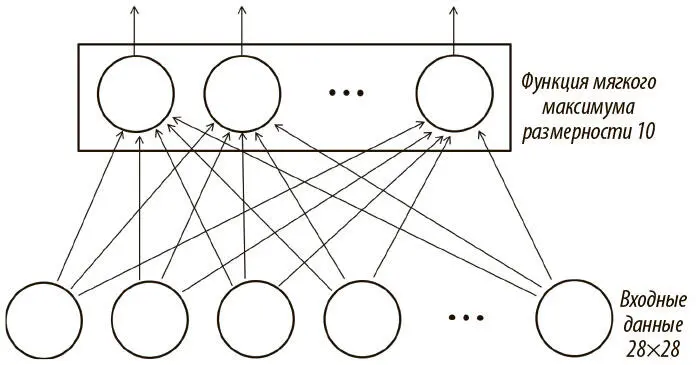
Рис. 3.4. Интерпретация логистической регрессии как примитивной нейросети

Легко заметить, что сеть для интерпретации логистической регрессии довольно примитивна. У нее нет скрытых слоев, а следовательно, ее способность усваивать сложные взаимоотношения ограничена. У нас есть выходная функция мягкого максимума размерности 10, поскольку у нас 10 возможных исходов для каждого входного значения. Более того, есть входной слой размера 784 — один входной нейрон для каждого пиксела изображения! Модель в целом способна корректно классифицировать наш набор данных, но еще есть куда расти. До конца этой главы и в главе 5 мы будем стараться повысить точность нашей работы. Но сначала посмотрим, как реализовать эту логистическую сеть в TensorFlow, чтобы обучить ее на нашем компьютере.

Модель логистической регрессии строится в четыре этапа:

1) inference: создается распределение вероятностей по выходным классам для мини-пакета [34];

2) loss: вычисляется значение функции потерь (в нашем случае перекрестная энтропии);

3) training: отвечает за вычисление градиентов параметров модели и ее обновление;

4) evaluate: определяется эффективность модели.

Для мини-пакета из 784-мерных векторов, соответствующих изображениям MNIST, мы можем выразить логистическую регрессию через функцию мягкого максимума от входных данных, умноженных на матрицу, которая представляет веса соединений входного и выходного слоев.

Каждая строка выходного тензора содержит распределение вероятностей по классам для соответствующего образца данных в мини-выборке:

def inference(x):

tf.constant_initializer(value=0)

W = tf.get_variable("W", [784, 10], initializer=init)

b = tf.get_variable("b", [10], initializer=init)

output = tf.nn.softmax(tf.matmul(x, W) + b)

return output

Теперь, с правильными метками для мини-пакета, мы можем вычислить среднюю ошибку на образец данных. При этом применяется следующий фрагмент кода, который вычисляет перекрестную энтропию по всему мини-пакету:

def loss(output, y):

dot_product = y * tf.log(output)

# Reduction along axis 0 collapses each column into a

# single value, whereas reduction along axis 1 collapses

# each row into a single value. In general, reduction along

# axis i collapses the ith dimension of a tensor to size 1.

xentropy = — tf.reduce_sum(dot_product, reduction_indices=1)

loss = tf.reduce_mean(xentropy)

return loss

Теперь, имея значение потерь, мы вычисляем градиенты и модифицируем наши параметры соответственно. TensorFlow облегчает процесс, обеспечивая доступ к встроенным оптимизаторам, которые выдают специальную операцию обучения. Ее можно запустить в сессии для минимизации ошибок. Отметим, что, создавая операцию обучения, мы передаем переменную, которая отражает количество обрабатываемых мини-выборок. Каждый раз, когда операция запускается, растет эта переменная, и мы можем отслеживать процесс:

def training(cost, global_step):

optimizer = tf.train.GradientDescentOptimizer(learning_rate)

train_op = optimizer.minimize(cost, global_step=global_step)

return train_op

Наконец, мы можем создать простой вычислительный подграф для оценки модели на проверочных или тестовых данных:

def evaluate(output, y):

correct_prediction = tf.equal(tf.argmax(output, 1) tf.argmax(y, 1))

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

return accuracy

На этом настройка графа в TensorFlow для модели логистической регрессии завершена.

У нас есть все компоненты, можно сводить их воедино. Чтобы сохранять важную информацию в процессе обучения модели, мы записываем в журнал несколько сводок статистики. Например, мы используем команды tf.scalar_summary [35]и tf.histogram_summary [36]для записи ошибки в каждом мини-пакете, ошибки на проверочном множестве и распределения параметров. Для примера приведем скалярную сводку статистик для функции потерь:

def training(cost, global_step):

tf.scalar_summary("cost", cost)

optimizer = tf.train.GradientDescentOptimizer(learning_rate)

train_op = optimizer.minimize(cost, global_step=global_step)

return train_op

На каждой эпохе мы запускаем tf.merge_all_summaries [37], чтобы собрать все записанные сводки, и с помощью tf.train.SummaryWriter сохраняем журнал на диске. В следующем разделе мы расскажем, как визуализировать эти журналы при помощи встроенного инструмента TensorBoard.

Помимо сводок статистики, мы сохраняем параметры модели с помощью tf.train.Saver. По умолчанию это средство поддерживает пять последних контрольных точек, которые мы можем восстанавливать для дальнейшего использования. В результате получаем следующий скрипт на Python:

# Parameters

learning_rate = 0.01

training_epochs = 1000

batch_size = 100

display_step = 1

with tf.Graph(). as_default():

# mnist data image of shape 28*28=784

x = tf.placeholder("float", [None, 784])

# 0–9 digits recognition => 10 classes

y = tf.placeholder("float", [None, 10])

output = inference(x)

cost = loss(output, y)

global_step = tf.Variable(0, name='global_step', trainable=False)

train_op = training(cost, global_step)

eval_op = evaluate(output, y)