Инесса Бурханова - Теория статистики

Значение выборочного метода: при минимальной численности исследуемых единиц проведение статистического исследования будет происходить в более короткие промежутки времени и с наименьшими затратами средств и труда.

В генеральной совокупности доля единиц, которая обладает изучаемым признаком, называется генеральной долей (обозначается р),а средняя величина изучаемого варьирующего признака – это генеральная средняя (обозначается х).

В выборочной совокупности долю изучаемого признака называют выборочной долей, или частью (обозначается w),средняя величина в выборке – это выборочная средняя.

Если в период обследования будут соблюдены все правила его научной организации, то выборочный метод даст довольно точны результаты, и поэтому данный метод целесообразно применять для проверки данных сплошного наблюдения.

Изучаемая статистическая совокупность состоит из единиц с варьирующими признаками. Состав выборочной совокупности может отличаться от состава генеральной совокупности, это расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки.

Ошибки, свойственные выборочному наблюдению, характеризуют размер расхождения между данными выборочного наблюдения и всей совокупности. Ошибки, возникающие в ходе выборочного наблюдения, называются ошибками репрезентативности и делятся на случайные и систематические.

Если выборочная совокупность недостаточно точно воспроизводит всю совокупность из-за несплошного характера наблюдения, то это называют случайными ошибками, и их размеры определяются с достаточной точностью на основании закона больших чисел и теории вероятностей.

Размер ошибки выборки и методы ее определения зависят от вида и схемы отбора.

Различают четыре вида отбора совокупности единиц наблюдения.

1. Случайный отбор– наиболее распространенный способ отбора в случайной выборке, его еще называют методом жеребьевки, при нем на каждую единицу статистической совокупности заготовляется билет с порядковым номером. Далее в случайном порядке отбирается необходимое количество единиц статистической совокупности. При этих условиях каждая из них имеет одинаковую вероятность попасть в выборку, например тиражи выигрышей, когда из общего количества выпущенных билетов в случайном порядке наугад отбирается определенная часть номеров, на которые приходятся выигрыши. При этом всем номерам обеспечивается равная возможность попасть в выборку.

2. Механический отбор– когда вся совокупность разбивается на однородные по объему группы по случайному признаку, потом из каждой группы берется только одна единица. Все единицы изучаемой статистической совокупности предварительно располагаются в определенном порядке, но в зависимости от объема выборки механически через определенный интервал отбирается необходимое количество единиц.

3. Типический отбор.Исследуемая статистическая совокупность разбивается по существенному, типическому признаку на качественно однородные, однотипные группы, затем из каждой этой группы случайным способом отбирается определенное количество единиц, пропорциональное удельному весу группы во всей совокупности. Типический отбор дает более точные результаты, так как при нем в выборку попадают представители всех типических групп.

4. Серийный (гнездовой) отбор.Отбору подлежат целые группы (серии, гнезда), отобранные случайным или механическим способом. По каждой такой группе, серии проводится сплошное наблюдение, а результаты переносятся на всю совокупность.

Точность выборки зависит и от схемы отбора. Выборка может быть проведена по схеме повторного и бесповторного отбора.

Повторный отбор.Каждая отобранная единица или серия возвращается во всю совокупность и может вновь попасть в выборку. Это так называемая схема возвращенного шара.

Бесповторный отбор.Каждая обследованная единица изымается и не возвращается в совокупность, поэтому она не попадает в повторное обследование. Эта схема получила название невозвращенного шара.

Комбинированный отборможет проходить одну или несколько ступеней. Выборка называется одноступенчатой, если отобранные однажды единицы совокупности подвергаются изучению.

Выборка называется многоступенчатой, если отбор совокупности проходит по ступеням, последовательным стадиям, причем каждая ступень, стадия отбора имеет свою единицу отбора. Многофазная выборка – на всех ступенях выборки сохраняется одна и та же единица отбора, но проводится несколько стадий, фаз выборочных обследований, которые различаются между собой широтой программы обследования и объемом выборки.

Собственнослучайная выборка– это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом. Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор, кроме случая.

Доля выборки– это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

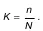
В собственнослучайный отборе заключаются и реализуются основные принципы выборочного статистического наблюдения.

Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.

Выборочная доля w,или частность, определяется отношением числа единиц, обладающих изучаемым признаком m,к общему числу единиц выборочной совокупности п.

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.

Ошибка выборки, ее еще называют ошибкой репрезентативности, представляет собой разность соответствующих выборочных и генеральных характеристик:

1) для средней количественного признака: ех = \х – х\;

2) для доли (альтернативного признака): ew = \х – p\.

Только выборочным наблюдениям присуща ошибка выборки.

Выборочная средняя и выборочная доля– это

случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.

Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Средняя ошибка выборки зависит от степени варьирования изучаемого признака.