Инесса Бурханова - Теория статистики
- Название:Теория статистики
- Автор:
- Жанр:
- Издательство:Конспекты, шпаргалки, учебники «ЭКСМО»b4455b31-6e46-102c-b0cc-edc40df1930e
- Год:2007
- Город:Москва
- ISBN:978-5-699-24184-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Инесса Бурханова - Теория статистики краткое содержание
Студенту без шпаргалки никуда! Удобное и красивое оформление, ответы на все экзаменационные вопросы ведущих вузов России.
Теория статистики - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Ординальная (порядковая) переменная помогает упорядочивать статистически исследованные объекты по степени проявления в них анализируемого свойства
Ранговая корреляция– статистическая связь между порядковыми переменными (измерение статистической связи между двумя или несколькими ранжировками одного и того же конечного множества объектов О 1,О 2,…, О п.
Ранжировка– это расположение объектов в порядке убывания степени проявления в них k-го изучаемого свойства. В этом случае x(k) называют рангом i-го объекта по k-му признаку. Раж характеризует порядковое место, которое занимает объект О i, в ряду п объектов.
К. Спирмен в 1904г предложил показатель, который служил для измерения степени тесноты связи между ранжировками
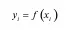
В последствии данный коэффициент был назван ранговым коэффициентом К. Спирмен:
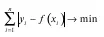
56. Методы регрессионного анализа
Термин «регрессия» ввел английский психолог и антрополог Ф.Гальтон.
Для точного описания уравнения регрессии необходимо знать чакон распределения результативного показателя у. В статистической практике обычно приходится ограничиваться поиском подходящих аппроксимаций для неизвестной истинной функции регрессии ffc), так как исследователь не располагает точным знанием условного закона распределения вероятностей анализируемого результатирующего показателя у при заданных значениях аргумента х.
Рассмотрим взаимоотношение между истинной f (х) = = М(у/х), модельной регрессией у и оценкой у регрессии. Пусть результативный показатель у связан с аргументом х соотношением:
у=2х 1,5+ε
где ε – случайная величина, имеющая нормальный закон распределения.
Причем M ε = 0 и d ε – σ 2. Истинная функция регрессии в этом случае имеет вид:
f(х) = М(у/х) = 2х i 1,5+ ε
Для наилучшего восстановления по исходным статистическим данным условного значения результативного показателя f(x) и неизвестной функции регрессии /(х) = М(у/х) наиболее часто используют следующие критерии адекватности(функции потерь).
Согласно методу наименьших квадратовминимизируется квадрат отклонения наблюдаемых значений результативного показателя y(i = 1, 2, ..., п) от модельных значений y i= f(х i), где х i– значение вектора аргументов в i-м наблюдении:
Σ(y i– f(х i)2 → min
Получаемая регрессия называется среднеквадратической.
Согласно методу наименьших модулей, минимизируется сумма абсолютных отклонений наблюдаемых значений результативного показателя от модульных значений:
y i = f(x i)
И получаем среднеабсолютную медианную регрессию:
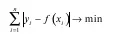
Регрессионный анализ– это метод статистического анализа зависимости случайной величины у от переменных х j(j=1,2, ..., k), рассматриваемых в регрессионном анализе как неслучайные величины, независимо от истинного закона распределения х j .
Интервал:
Закладка:










