Инесса Бурханова - Теория статистики

Индекс физического объема товарооборотапредставляет собой изменение физического объема в отчетном периоде по соотнесению с базисным. Чтобы агрегатный индекс показывал лишь изменение физического объема товарооборота, в качестве весов берутся неизменные цены базисного и отчетного периодов. Неизменные цены всегда только цены базисного периода. Применение в качестве весов неизменных цен дает возможность получить правильное представление о динамике физического объема товарооборота.

В индексе физического объема сомножитель индексируемого показателя берется на уровне базисного периода.

Абсолютное изменение физического объема вычисляется как разность между числителем и знаменателем индекса еq 1p 0– еq 0p 0.

Если индексы вычисляются за несколько периодов, то для всех них могут быть приняты одни и те же веса – индексы с постоянными весами, или же для каждого периода свои веса – индексы с переменными весами.

Теоретически возможны четыре типа индексов.

1. Общие базисные индексы цен с постоянными (базисными) весами:

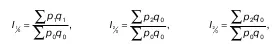
2. Общие базисные индексы цен с переменными (отчетными) весами:

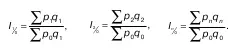
3. Общие цепные индексы цен с постоянными весами:

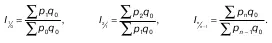
4. Общие цепные индексы цен с переменными весами:

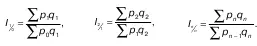
В этих индексах отражается как изменение цен за ряд последовательных периодов, так и изменение структуры реализованных товаров.

Для характеристики изменения цен по сравнению с начальным периодом без учета изменений в структуре произведенных товаров применяют общие базисные индексы с постоянными весами, в тех же целях, но с учетом изменения структуры – базисные индексы с переменными весами. Для определения изменения цен каждого периода по сравнению с предыдущим без учета изменений в структуре проданных товаров применяют цепные индексы с постоянными весами, с учетом изменений в структуре – цепные индексы с переменными весами.

Выбор периода взвешивания индексов зависит от того, какие индексы вычисляются: индексы количественных (объемных) или качественных показателей.

1. Индекс себестоимости продукциипоказывает, во сколько раз себестоимость в отчетном периоде в среднем выше или ниже базисной или плановой себестоимости, а также абсолютный размер экономии или перерасхода в результате изменения себестоимости. Индекс себестоимости – это индекс качественных показателей и исчисляется по весам (объему) продукции отчетного периода:

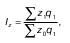
где z 1 – себестоимость единицы продукции в отчетном периоде;

z 0– себестоимость единицы продукции в базисном (или плановом) периоде;

q1 – количество продукции в отчетном периоде.

2. Индекс производительности труда.Производительность труда определяется количеством продукции, произведенной в единицу времени, или затратами рабочего времени на производство единицы продукции. Для определения изменения производительности труда в отчетном периоде по сравнению с базисным нужно затраты рабочего времени на производство единицы продукции в базисном периоде (t 0)разделить на затраты рабочего времени на производство единицы продукции в отчетном периоде (t 1).

Индивидуальный индекс производительности труда равен:

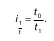
Для построения агрегатного индекса производительности труда необходимо затраты рабочего времени на производство одной единицы продукции взвесить на количество продукции, произведенной в отчетном периоде:

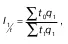
где t 1q 1– фактические затраты времени на производство всей продукции в отчетном периоде;

t 0q 1показывает, сколько времени потребовалось затратить на производство всей продукции отчетного периода в базисном периоде.

3. Индекс трудоемкостихарактеризует модификацию трудоемкости единицы продукции в отчетном периоде по сопоставлению с базисным. Величина индекса трудоемкости обратно пропорциональна величине индекса производительности труда, вычисленной по затратам времени на производство единицы продукции. Формула индивидуального индекса:

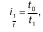
а агрегатного:

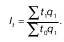
Индекс трудоемкости – это индекс качественных показателей, и рассчитывается он также по весам отчетного периода.

1. Индекс выполнения плана.При его вычислении фактические данные сопоставляются с плановыми, причем весами индекса могут быть показатели плановые и фактические.

2. Среднеарифметический и среднегармониче-ский индексы.

Агрегатные индексы цен, физического объема товарооборота и другие могут быть рассчитаны, если известны индексируемые величины и веса, т. е. p и q. Допустим, что имеется произведение pq и индивидуальные индексы. Возникает проблема построения средних индексов, идентичных агрегатным, путем осреднения индивидуальных индексов.

Преобразование агрегатного индекса в среднеарифметический можно рассмотреть на примере агрегатного индекса физического объема товарооборота.

В данном случае индивидуальные индексы должны быть взвешены на базисные соизмерители. Из индивидуального индекса физического объема товарооборота i q= q 1/ q 0следует, что q 1= i q/ q 0.

Если заменить q 1в числителе агрегатного индекса физического объема товарооборота

I q= Σq 1p 0/ Σq 0p 0, на i q/q 0,

то получим I q= Σi qq 0p 0/ Σq 0p 0.

Это среднеарифметический индекс физического объема товарооборота.

Но если не известны отдельные значения q 1и p 1, а дано их произведение q 1p 1– товарооборот отчетного периода и индивидуальные индексы цен i p= Р 1/ /р 0, и сводный индекс рассчитывается с отчетными весами, то применяется среднегармонический индекс цен.Необходимо, чтобы индивидуальные индексы были взвешены так, чтобы среднегармонический индекс совпал с агрегатным. Из формулы i p= Р 1/ Р 0определяем неизвестное значение р 0и, заменив в формуле агрегатного индекса цен I p= Σq 1p 1/ Σq0p0 значение Р 0= Р 1/ i p, получаем I p= Σp 1q 1/ Σ(p 1/ i p)q 1=Σp 1q 1/ Σ(p 1q 1/ i p)