Деннис Шервуд - Видеть лес за деревьями. Системный подход для совершенствования бизнес-модели

Представьте себе, что я на секунду отвлекся, пока наливал кофе в чашку. Что произойдет? Какие действия я предприму? Как они будут связаны с диаграммой цикличной причинности? И как тогда будет выглядеть график поведения реального уровня кофе в чашке ?

Это не такое простое упражнение, особенно третий вопрос, касающийся диаграммы цикличной причинности, поэтому хорошенько подумайте.

Как вы помните, в качестве планируемого уровня кофе у нас задано полчашки, поэтому, если я отвлекусь хотя бы на секунду, я налью больше, но, вероятно, замечу это прежде, чем кофе перельется через край. Что произойдет дальше? Я осторожно наклоню чашку и вылью лишний кофе, но если я опять буду неосторожен, то могу наклонить ее слишком сильно, и тогда мне придется опять доливать кофе. В конце концов, переливая кофе туда-сюда, я добьюсь нужного мне уровня.

Как эти действия будут связаны с диаграммой цикличной причинности? Начнем с того момента, когда я заметил, что налил кофе больше половины чашки, и остановился. В этот момент реальный уровень кофе в чашке выше планируемого. Если я определю разницу между планируемым и реальным уровнемкак планируемый уровень минус реальный, то получу отрицательное число . Причем чем больше я превышу уровень, тем большим будет это отрицательное число. Двигаясь по петле, мы увидим, что связь типа П, соединяющая разницу между планируемым и реальным уровнеми физическое действие, демонстрирует движение эти двух элементов в одном направлении. По мере того как разница между планируемым и реальным уровнемвсе больше уходит «в минус», то же самое происходит и с физическим действием. Но что может означать «отрицательное физическое действие»? Если положительное физическое действие означает наливание кофе в чашку, то отрицательное может означать только одно: выливание из чашки. Получается, что диаграмма цикличной причинности предвосхищает события и говорит нам, что делать: отрицательное значение разницы между планируемым и реальным уровнемподсказывает нам, что кофе надо выливать.

Это тоже связь типа П, связывающая физическое действиес реальным уровнем кофе в чашке, поэтому, если физическое действиеявляется отрицательным, его влияние на реальный уровень кофе в чашкетоже отрицательное. Это подразумевает уменьшение реального уровня, что, конечно же, верно, поскольку мы выливаем кофе из чашки.

Предупреждение: далее следует часть, которую многие считают слишком сложной. Диаграмма цикличной причинности показывает связь типа О между реальным уровнем кофе в чашкеи разницей между планируемым и реальным уровнем.Это означает, что они движутся в противоположных направлениях. Поэтому если реальный уровень кофе в чашкеуменьшается, разница между планируемым и реальным уровнемдолжна увеличиваться, стремиться «в плюс», то есть становиться «более положительной» (как вы помните, вначале она была отрицательной). Если это число увеличивается и становится все «более положительным», оно должно становиться «менее отрицательным» и приближаться к нулю.

Система опять стремится к цели наполнить чашку наполовину.

Мало кто понимает это с первого раза. Поэтому не спеша перечитайте все еще раз. Смысл в том, что при строгом описании поведения петли всем элементам приписаны количественные значения, и все они имеют знак «плюс» или «минус». Обычно когда они имеют знак «плюс», мы не задумываемся об этом или даже не замечаем этого. Во всех предыдущих примерах подразумевалось, что все элементы имеют знак «плюс». Это первый пример, где некоторые элементы имеют знак «минус», и бывает трудно сообразить, что, когда вы увеличиваете отрицательное число (скажем –3), вы делаете его более положительным (оно становится –2), а не более отрицательным (оно не становится –4).

Теперь давайте предположим, что я нечаянно вылил слишком много, и теперь реальный уровень кофе в чашкениже планируемого. Таким образом, разница между планируемым и реальным уровнем– положительное число, и я выполняю положительное физическое действие, поскольку мы имеем связь типа П. Это означает, что я наливаю кофе обратно, что логично. На реальный уровень кофе в чашкеоказывается положительное влияние (опять связь типа П), и он опять повышается, что тоже логично. Рост реального уровня кофе в чашкевызывает сокращение разницы между планируемым и реальным уровнем(связь типа О). Тот факт, что разница между планируемым и реальным уровнемстановится меньше, предполагает, что система стремится к своей цели.

Происходящее гораздо легче оценить с помощью графика, демонстрирующего несколько преувеличенную форму поведения реального уровня кофе в чашкево времени (рис. 6.3).

Этот график наглядно демонстрирует постепенное повышение и понижение реального уровня кофе в чашке, стремящегося к планируемому. Планируемый уровень отмечен с помощью соответствующего свободного звена, и свободные звенья, выполняющие подобные функции, известны как свободные звенья планируемых показателей , которые отличаются от свободных звеньев, с которыми мы уже встречались прежде.

Уравновешивающие петли стремятся к планируемым показателям или целям. Иногда они явно выражены с помощью свободных звеньев планируемых показателей, иногда нет, но любая уравновешивающая петля стремится к цели. Иногда движение к цели происходит плавно, но, если в системе имеются задержки, движение может быть скачкообразным.

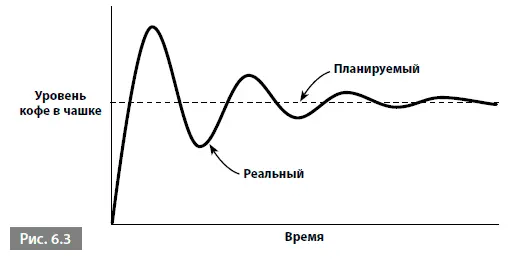
И опять мы видим объединяющий принцип. Все уравновешивающие петли стремятся к цели, одна и та же диаграмма цикличной причинности может вести к плавному движению к цели (как показано на рис. 6.2) или скачкообразному. Разница между этими двумя типами поведения определяется тем, насколько быстро система реагирует на сигнал. Если мгновенно, поведение обычно бывает плавным. Если же в системе имеются задержки во времени (как в примере, когда наливающий кофе отвлекается), то она будет вести себя скачкообразно.

Пример с чашкой кофе хорошо иллюстрирует плавное движение к цели. Но он выглядит несколько искусственно, когда речь идет о скачкообразном движении, ведь едва ли кто-то может быть настолько неуклюж. Однако в повседневной жизни встречается множество примеров скачкообразного поведения.