Кристина Нестерова - Фискальная политика в многострановой модели общего экономического равновесия

Миграция в модели также предполагается экзогенной. В каждом периоде популяция увеличивается за счет мигрировавших агентов, при этом возрастная структура, а также класс производительности мигрантов зависят от региона. Для сохранения гомогенности популяции делается предположение, в соответствии с которым распределение всех характеристик в группе прибывающих в некотором периоде мигрантов совпадает с соответствующим распределением этих характеристик во всей популяции. Все вероятностные распределения, определяющие динамику рождения детей и смертность, переносятся с основной популяции на мигрантов.

Предпочтения домохозяйств отражаются приведенной ниже сепарабельной функцией полезности, которая предполагает как компоненту, связанную с собственным потреблением и досугом, так и компоненту, соответствующую потреблению детей, которых поддерживает агент. Общая полезность агента выражается функцией U ( a, t, k ), где t является индексом времени, a обозначает возраст агента в годах, а k соответствует классу производительности, к которому принадлежит агент. Компоненту полезности от собственного потребления и досуга обозначим через V ( a, t, k ), а полезность от потребления всех детей данного агента обозначим через H ( a, t, k ). Таким образом,

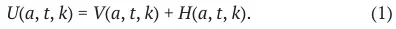
Спецификация для функции собственной полезности следующая:

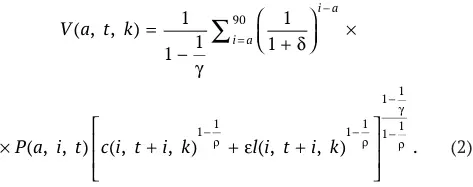
Уровень потребления агента, относящегося к когорте возраста а и принадлежащего к классу продуктивности к, в периоде t обозначен через с(а, t, к). Время, которое данный агент тратит на досуг, обозначено через l(а, t, к), а е является специальным параметром полезности от индивидуального досуга. Однопериодная функция полезности агента является CES -функцией от потребления и времени индивидуального досуга, а соответствующий параметр внутривременной эластичности замещения обозначен через р. Вероятность, с которой агент, чей возраст в периоде t равен а, доживет до периода i , обозначена через Р(а, i, t). Смертность в модели не зависит от класса продуктивности агента. Параметры δ и γ характеризуют межвременные предпочтения домохозяйств.

Общая собственная полезность агента, таким образом, равна сумме взвешенных CES -агрегаторов будущего потребления и досуга, а взвешивающими множителями выступают вероятности дожития и факторы временных предпочтений.

Полезность, которую агент получает от уровня потребления его детей, имеет вид, сходный с видом функции собственной полезности. Так в полезность родителя входит дисконтированная сумма полезности от будущего потребления всех его детей, включая тех, чье рождение ожидается в будущем. Вид соответствующей функции следующий:

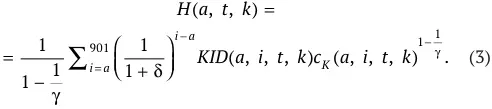
В периоде t рассмотрим агента, который относится к когорте возраста a и классу производительности k . Число детей, которые у него будут, когда агент достигнет возраста i , обозначим через KID ( a, i, t, k ), а потребление каждого ребенка – через c K ( a, i, t, k ).

Если ввести дополнительное обозначение d ( a, z, t ) для вероятности, с которой агент заданного поколения умрет в возрасте равном ровно z , то вероятность дожития P ( a, i, t ) можно представить в виде:

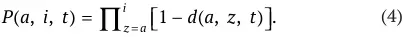
Совокупная стоимость активов, которыми в периоде t располагает агент, относящийся к классу производительности k и принадлежащий поколению возраста a , обозначим через A ( a, t , k). В каждом периоде агент получает доход от предложения труда, платит налоги и получает трансферты, получает наследство от родителя и затрачивает средства на собственное потребление и потребление своих детей. В соответствии с предположениями модели, в каждый период времени у агента есть общий запас времени, который он может распределить между досугом, входящим в его функцию полезности, и рабочим временем. Общий запас доступного времени обозначим как h ( a, t ), тогда время, которое агент будет предлагать на рынке труда, равно h ( a, t ) – l ( a, t, k ). Обозначив зарплату, выплачиваемую за единицу рабочего времени, через w ( t, k ), можно получить выражение для трудового дохода агента в виде:

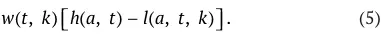
Общие затраты на потребление (собственное и потребление детей) представляются в виде:

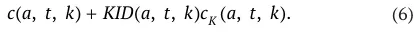
Наследство, полученное агентом, обозначим как I ( a, t, k ). Чистую стоимость уплачиваемых агентом налогов обозначим через T ( a, t, k ). Тогда, если обозначить ставку доходности как r ( t ), уравнение, описывающее динамику стоимости активов, принадлежащей выбранному агенту, можно записать следующим образом:

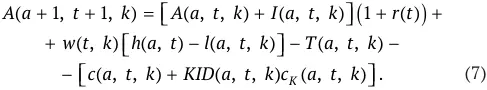
Активы, находившиеся в собственности всех умерших агентов в рамках одного класса производительности, суммируются в общий пул и затем распределяются среди живущих агентов этого класса в возрасте от 23 до 67 лет. Если общая стоимость пула активов равна A ( t, k ), то вся когорта агентов в возрасте l получает долю Г( l, t ) этого пула и эти активы равномерно распределяются среди членов когорты, численность которой обозначена как N ( l, t, k ). Соответственно, данные доли суммируются к единице по всем указанным возрастам:

При этом распределение Г( l, t ) соответствует распределению по возрастам всех детей агентов, умерших в данном году. Правило, в соответствии с которым агент из когорты возраста l получает долю наследства, задается формулой:

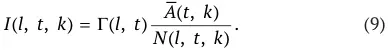
Технический прогресс задается через повышение эффективности труда со временем. Этот эффект моделируется нами следующим образом. Предполагается, что общий запас времени, которое агент может распределять между досугом и трудом, увеличивается с одинаковым ежегодным темпом λ. Это может быть интерпретировано как то, что постепенно с течением времени рабочая сила становится более продуктивной (см. [6]). С учетом введенного ранее обозначения h ( a, i ) для общего запаса времени, которым располагает агент возраста a в периоде i , технический прогресс задается правилом: