Никита Сергеев - Аналитика и Data Science. Для не-аналитиков и даже 100% гуманитариев…

Генерал выше полковника. Работа может быть интересна, безразлична или неинтересна. Занявший I место по бегу выше II и III (хотя разница в их абсолютном результате могла составить между ними всего 5 секунд).

Эту шкалу, как и номинальную, используют для классификации объектов и подсчета количества или %. Но по ней можно применять уже и не только частотный анализ – к примеру, можно попробовать найти связь между частотой использования мата и воинским званием.

Третий тип – количественные\интервальные шкалы( рис. 14 ).

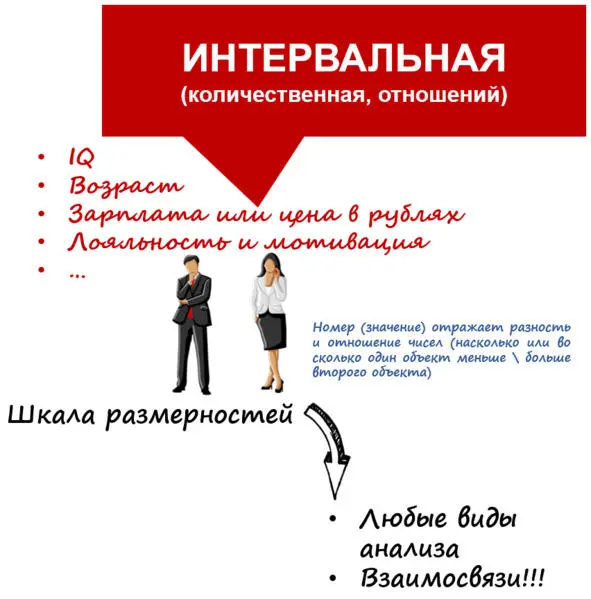
Рис. 14. Интервальная (количественная, относительная, метрическая) шкала

Если предыдущая порядковая шкала несла инфо о порядке данных, то количественная – это числа, реально отражающие размерности, разности, масштабы и расстояния между объектами.

Например, точное время, за которое бегуны пробежали дистанцию. Возраст лет. IQ. Уровень лояльности или мотивации сотрудника. Доход.

С этими шкалами можно осуществлять любые виды анализа. Более того, их можно легко превращать в порядковые, объединяя диапазоны значений. Например, доход можно разбить на 4 диапазона – низкий, средний, выше среднего и высокий.

Оговорюсь, что количественные (метрические) шкалы могут выглядеть по-разному: есть с отрицательными значениями, есть с абсолютным нулем (например, возраст) есть те, которые в принципе не начинаются с нуля (например, IQ). Аналитики в разговорах, статьях, литературе их могут именовать по-разному (например, интервальная, шкала масштаба или шкала отношений с абсолютным нулем…) – но, по сути, все они с точки зрения использования методов аналитического инструментария одинаковы.

Когда говорят слово гипотеза, у многих возникает ассоциация с учеными или теориями. На самом деле гипотезами оперируют и менеджеры, бизнесмены, сотрудники компаний, криминалисты и т. д.

Например, создавая рекламную кампанию, менеджер по рекламе выдвигает гипотезу, почему и как реклама должна сработать – и на их базе строит свою кампанию. Бизнесмен, принимая решение вкладываться в дело или нет, выдвигает и размышляет над целым набором гипотез-предположений. Криминалист, расследуя перестрелку, выдвигает гипотезы, которые проверяются в ходе расследования и изучения фактов.

Например, я при проведении исследований персонала проверяю гипотезу, что определенный набор организационных факторов (зарплата, карьера, обучение и развитие, морально-психологический климат и т.д.) влияет на лояльность и мотивацию персонала.

Или прогнозируя будет кандидат успешным продавцом или нет в конкретной компании, в качестве гипотезы могу заложить предположение, что успешность определяют результаты по нескольким тестам, пол и уровень образования.

Гипотезы очень важны. Хорошо о них было сказано на 32 минуте последней сериии фильма «Михайло Ломоносов» (Мосфильм, 1986): «Запомните, в основе науки лежит ежечасная работа по спирали опыта. Но не бойтесь и гипотез! Они в естественных и философских трудах подчас единственный путь, которым величайшие умы постигли самых важных истин. Гипотезы! Полет! Порыв души!…»

Гипотезы могут или быть верными, или отклоняться.

И в современных подходах отклонить или принять гипотезу помогает расчет вероятности, являются наблюдаемые закономерности случайными, или можно считать их реальными. Особенно это важно для социально-экономической реальности, где не работают жестко предопределенные законы.

Так, например, для успешности продавца могут оказаться верными предположения по тестам и уровню образования, но будет отвергнуто влияние пола.

Любая гипотеза (наше предположение) в статистике раскладывается на две статистических гипотезы:

– нулевая (H 0), которая гласит, что обнаруженных в наборе данных (выборке) закономерностей в генеральной совокупности нет – это исключительно случайность, которая имеет место только в исследуемой Вами выборке.

– альтернативная (H 1), которая гласит противоположное: что обнаруженная в выборке закономерность имеет место и в генеральной совокупности.

Пока о гипотезах все. Больше о нулевых и альтернативных гипотез будут рассмотрены в следующей главе в привязке к понятию вероятности.

Вероятность в статистике выражается в % и лежит в диапазоне от 0 до 1 (0—100%). Обозначается буквой Р – от англ. probability .

В повседневной жизни мы привыкли оценивать вероятность события или вероятность истинности каких-то утверждений. Например, 80% что пойдет дождь, 99% что я сдам этот тест, вероятность выбить с клиента долг менее 10%…

Но практическая статистика оперирует не вероятностью наступления события (или истинности утверждения), а вероятностью ошибиться в случае применения обнаруженной закономерности ко всей генеральной совокупности.

Самым страшным и критичным в анализе считается именно обнаружить закономерности, взаимосвязи или различия, которых на самом деле в генеральной совокупности не существует.

А не обнаружить какие-то реально существующие взаимосвязи – это не так страшно. Это как в правосудии: выпустить виновного считается менее критичным, нежели обвинить невиновного…

Статисты придали этим вещам названия в виде нулевой (H 0)и альтернативной (H 1)гипотез. H 0говорит, что обнаруженных закономерностей, взаимосвязей или отличий в генеральной совокупности нет – это исключительно случайность, которая имеет место только в исследуемой Вами выборке.

Я в свое время для себя просто запомнил, что нулевая гипотеза (H 0) – это ноль различий / взаимосвязей / закономерностей.

Только если вероятность H 0крайне низка – принимается альтернативная гипотеза (H 1), что обнаруженная в выборке закономерность имеет место и в генеральной совокупности.

Т.е., в практике мы пытаемся в первую очередь ответить на вопрос – какова вероятность, что выведенная нами взаимосвязь между параметрами или закономерность является случайной и ее на самом деле нет в генеральной совокупности?

Например, криминалист, собрав все известные случаи, видит вроде как закономерность, что серийные маньяки орудуют в пределах трех кварталов от места жительства. Можно ли это распространить на всю генеральную совокупность? Или это просто случайное «стечение обстоятельств» в его выборке данных?

Конечно, проще всего было бы взять еще пару выборок из генеральной совокупности и убедиться, что в них также наблюдается такая связь. Но это не всегда возможно. И все равно ответ не может быть точным, пока не будет изучена вся генеральная совокупность.