Александр Харчевников - Социальный метаболизм. Полилогический матричный анализ «обменных процессов» и стоимости

Наконец, действительными числами f ijобозначим заданное количество производства продуктов j-го вида i-ым агентом-производителем. При этом, согласно начальным условиям, структура потребления продуктов каждого из агентов-потребителей равна структуре производства, а объёмы потребления каждого из агентов равны между собой. Само распределение производства продуктов между агентами-производителями дано в форме матрицы на рисунке 12.

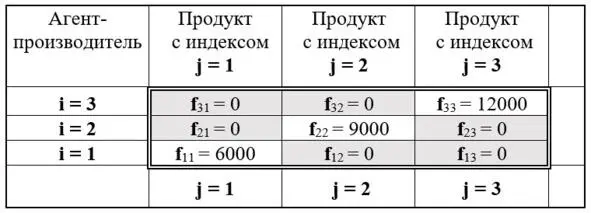
Рис. 12. Матрица производства продуктов агентами-производителями

Соответственно, на рисунке 13 представлена трёхмерная балансовая матрица, элементы которой количественно описывают один цикл кругооборота «обмена (обращения)». Элементами этой балансовой матрицы являются неизвестные переменные x ijk, величину которых нам необходимо и определить. Это позволит выявить меновые отношения, которые в совокупности отражают равновесное состояние некого условного общества, ранее взятого в качестве иллюстративного примера (см. рис.1 и рис.12).

Для удобства восприятия матрица изображена в виде трёх вертикальных фронтальных срезов. Каждый из срезов отображает частную плоскостную двухмерную матрицу «обмена» по одному из j-ых видов продуктов между i-ыми и k-ыми агентами воспроизводственного процесса действительной жизни этого общества.

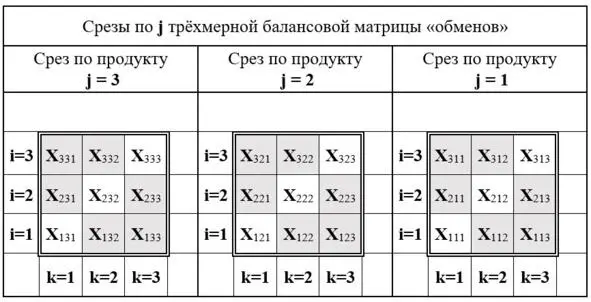
Рис. 13. Трёхмерная балансовая матрица «производство – потребление»

Таким образом, для полного количественного описания одного цикла кругооборота «обмена (обращения)» необходимо определить численные значения всех 27 неизвестных переменных x ijk. В принятых обозначениях количественные (численные) исходные данные для этой задачи даны в матричной таблице рисунка 12.

Обозначим общий суммарный объём производства j—го продукта всеми агентами производства через F j. Тогда, с учётом данных матрицы рисунка 12, отражающих численные значения заданного количества производства продуктов j-го вида i-ым агентом-производителем как величину f ij, получим следующие три равенства (уравнения):

F j=1 = f 11+ f 21+ f 31= 6000 +0 +0 = 6000; (1)

F j=2 = f 12+ f 22+ f 32= 0 +9000 +0 = 9000; (2)

F j=3 = f 13+ f 23+ f 33= 0 +0 +12000 = 12000. (3)

Если это выразить в неизвестных переменных x ijk, имея ввиду, что объём производства f ijкаждого j—го продукта i-ым агентом, равен сумме объёмов, получаемых всеми агентами (и самим производителем) x ijk, то получим следующие уравнения.

Для продукта j=1:

f 11= x 111+ x 112+ x 113= 6000, (4) *

f 21= x 211+ x 212+ x 213= 0, (5) *

f 31= x 311+ x 312+ x 313= 0. (6) *

Для продукта j=2:

f 12= x 121+ x 122+ x 123= 9000, (7) *

f 22= x 221+ x 222+ x 223= 0, (8) *

f 32= x 321+ x 322+ x 323= 0. (9) *

Для продукта j=3:

f 13= x 131+ x 132+ x 133= 12000, (10) *

f 23= x 231+ x 232+ x 233= 0, (11) *

f 33= x 331+ x 332+ x 333= 0. (12) *

Далее, исчислим структуру производства как отношение (пропорция):

F j=1: F j=1: F j=1 =6000: 9000: 12000 = 2: 3: 4. (13)

Напомним, что по условиям задачи структура потребления равна структуре производства в целом для общества и по каждому агенту-потребителю.

Следовательно, для агента-потребителя с индексом k = 1 имеем:

F j=1: F j=2: F j=3 = (x 111+ x 211+ x 311 ): (x 121+ x 221+ x 321 ): (x 131+ x 231+ x 331 ). (14)

Таким образом получаем следующую пропорцию (отношение):

(x 111+ x 211+ x 311 ): (x 121+ x 221+ x 321 ): (x 131+ x 231+ x 331 ) = 2: 3: 4. (15)

Соответствующие полученному отношению в форме пропорции (15) линейные уравнения имеют вид:

(x 111+ x 211+ x 311 ) / (x 121+ x 221+ x 321 ) = 2/3, или иначе

3 × (x 111+ x 211+ x 311 )= 2 × (x 121+ x 221+ x 321 ); (16) *

(x 111+ x 211+ x 311 ) / (x 131+ x 231+ x 331 ) = 2/4, или иначе

2 × (x 111+ x 211+ x 311 )= 4 × (x 131+ x 231+ x 331 ); (17) *

(x 121+ x 221+ x 321 ) / (x 131+ x 231+ x 331 ) = 3/4, или иначе

4 × (x 121+ x 221+ x 321 )= 3 × (x 131+ x 231+ x 331 ). (18) *

Аналогично, для агента-потребителя с индексом k = 2 имеем:

F j=1: F j=2: F j=3 = (x 112+ x 212+ x 312 ): (x 122+ x 222+ x 322 ): (x 132+ x 232+ x 332 ). (19)

Таким образом получаем следующую пропорцию (отношение):

(x 112+ x 212+ x 312 ): (x 122+ x 222+ x 322 ): (x 132+ x 232+ x 332 ) = 2: 3: 4. (20)

Соответствующие полученному отношению в форме пропорции (20) линейные уравнения имеют вид:

(x 112+ x 212+ x 312 ) / (x 122+ x 222+ x 322 ) = 2/3, или иначе

3 × (x 112+ x 212+ x 312 )= 2 × (x 122+ x 222+ x 322 ); (21) *

(x 112+ x 212+ x 312 ) / (x 132+ x 232+ x 332 ) = 2/4, или иначе

2 × (x 112+ x 212+ x 312 )= 4 × (x 132+ x 232+ x 332 ); (22) *

(x 122+ x 222+ x 322 ) / (x 132+ x 232+ x 332 ) = 3/4, или иначе

4 × (x 122+ x 222+ x 322 )= 3 × (x 132+ x 232+ x 332 ). (23) *

Аналогично, для агента-потребителя с индексом k = 3 имеем:

F j=1: F j=2: F j=3 = (x 113+ x 213+ x 313 ): (x 123+ x 223+ x 323 ): (x 133+ x 233+ x 333 ). (24)

Таким образом получаем следующую пропорцию (отношение):

(x 113+ x 213+ x 313 ): (x 123+ x 223+ x 323 ): (x 133+ x 233+ x 333 ) = 2: 3: 4. (25)

Соответствующие полученному отношению в форме пропорции (25) линейные уравнения имеют вид: