Александр Харчевников - Социальный метаболизм. Полилогический матричный анализ «обменных процессов» и стоимости

Так, например, содержащееся в настоящей задаче условие производства j-го продукта только одним i-ым агентом производства обращает целый ряд неизвестных переменных x ijkв ноль и сокращает необходимое для решения системы число линейных уравнений с 27 до 9. При этом исходное равенство переменных нулю достаточно просто и наглядно объясняется указанными специфическими, конкретными, условиями задачи.

В частности, на схеме рисунка 14, повторяющей три j-ых среза трёхмерной балансовой матрицы «обменов» рисунка 13, обозначения неизвестных переменных, равных нулю по указанным специфическим условиям задачи, заменены их значением « 0». Так, например, так как первый агент-производитель с индексом i = 1 производит только продукт с индексом j=1, то переменные x 131, x 132, x 133, x 121, x 122, x 123равны нулю (= 0). Очевидно, что этот агент-производитель не производит продукты с индексами j=2 и j=3, а поэтому и предложить их «к обмену» не может. Аналогично обстоит дело и с агентами-производителями i=2 и i=3,производящими только, соответственно, продукты j=2 и j=3.

Соответствующая система уравнений примет вид:

f 11= x 111+ x 112+ x 113= 6000, (4) * 1

f 21= 0 211 +0 2 12 +0 2 13 = 0, (5) * 2

f 31= 0 311 +0 3 12 +0 3 13 = 0, (6) * 3

f 12= 0 121 +0 1 22 +0 1 23 = 0, (7) * 4

f 22= x 221+ x 222+ x 223= 9000, (8) * 5

f 32= 0 321 +0 3 22 +0 3 23 = 0, (9) * 6

f 13= 0 131 +0 1 32 +0 1 33 = 0, (10) * 7

f 23= 0 231 +0 2 32 +0 2 33 = 0, (11) * 8

f 33= x 331+ x 332+ x 333= 12000, (12) * 9

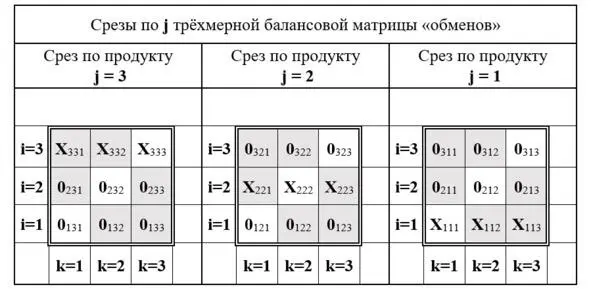
Рис. 14. Балансовая матрица, повторяющая три j-ых среза трёхмерной матрицы «обменов» рисунка 13, с обозначениями неизвестных переменных и переменных равных нулю

3 × (x 111+0 2 11 +0 3 11 )= 2 × (0 121 + x 221+0 3 21 ), (16) * 10

2 × (x 111+0 2 11 +0 3 11 )= 4 × (0 131 +0 2 31 + x 331 ), (17) * 11

4 × (0 121 + x 221+0 3 21 )= 3 × (0 131 +0 2 31 + x 331 ), (18) * 12

3 × (x 112+0 2 12 +0 3 12 )= 2 × (0 122 + x 222+0 3 22 ), (21) * 13

2 × (x 112+0 2 12 +0 3 12 )= 4 × (0 132 +0 2 32 + x 332 ), (22) * 14

4 × (0 122 + x 222+0 3 22 )= 3 × (0 132 +0 2 32 + x 332 ), (23) * 15

3 × (x 113+0 2 13 +0 3 13 )= 2 × (0 123 + x 223+0 3 23 ), (26) * 16

2 × (x 113+0 2 13 +0 3 13 )= 4 × (0 133 +0 2 33 + x 333 ), (27) * 17

4 × (0 123 + x 223+0 3 23 )= 3 × (0 133 +0 2 33 + x 333 ), (28) * 18

(x 111+0 2 11 +0 3 11 )= (x 112+0 2 12 +0 3 12 ), (32) * 19

(x 111+0 2 11 +0 3 11 )= (x 113+0 2 13 +0 3 13 ), (33) * 20

(x 112+0 2 12 +0 3 12 )= (x 113+0 2 13 +0 3 13 ), (34) * 21

(0 121 + x 221+0 3 21 )= (0 122 + x 222+0 3 22 ), (35) * 22

(0 121 + x 221+0 3 21 )= (0 123 + x 223+0 3 23 ), (36) * 23

(0 122 + x 222+0 3 22 )= (0 123 + x 223+0 3 23 ), (37) * 24

(0 131 +0 2 31 + x 331 )= (0 132 +0 2 32 + x 332 ), (38) * 25

(0 131 +0 2 31 + x 331 )= (0 133 +0 2 33 + x 333 ), (39) * 26

(0 132 +0 2 32 + x 332 )= (0 133 +0 2 33 + x 333 ). (40) * 27

В результате получаем, сохраняя (повторяя) при этом прежние номера соответствующих уравнений:

f 11= x 111+ x 112+ x 113= 6000, (4) * 1

f 22= x 221+ x 222+ x 223= 9000, (8) * 5

f 33= x 331+ x 332+ x 333= 12000, (12) * 9

3×x 111= 2×x 221, (16) * 10

2×x 111= 4×x 331, (17) * 11

4× x 221= 3×x 331, (18) * 12

3×x 112= 2×x 222, (21) * 13

2×x 112= 4×x 332, (22) * 14

4×x 222= 3×x 332, (23) * 15

3×x 113= 2×x 223, (26) * 16

2×x 113= 4×x 333, (27) * 17

4×x 223= 3×x 333, (28) * 18

x 111= x 112, (32) * 19

x 111= x 113, (33) * 20

x 112= x 113, (34) * 21

x 221= x 222, (35) * 22

x 221= x 223, (36) * 23

x 222= x 223, (37) * 24

x 331= x 332, (38) * 25

x 331= x 333, (39) * 26

x 332= x 333. (40) * 27

Таким образом сократилось не только число уравнений, но и число неизвестных ограничилось девятью переменными. Эти девять переменных полностью представлены в трёх уравнениях (4) * 1, (8) * 5 и (12) * 9. При этом остальные переменные могут быть выражены через эти девять, что видно по равенствам от (16) * 10 до (40) * 27. В результате и число уравнений, необходимых для получения решения стало равным девяти. Приведём ниже один из вариантов этих «необходимых» уравнений и численную оценку самих переменных.

Рассмотрим равенства (4) * 1, (32) * 19 и (33) * 20:

f 11= x 111+ x 112+ x 113= 6000, (4) * 1

x 111 = x 112, (32) * 19

x 111 = x 113. (33) * 20

Получаем очевидное решение для следующих трёх неизвестных переменных:

x 111= 6000/3 = 2000; x 112= 2000; x 113= 2000.

Далее, рассмотрим равенства (8) * 5, (35) * 22 и (37) * 24:

f 22= x 221+ x 222+ x 223= 9000, (8) * 5

x 221 = x 222, (35) * 22

x 222 = x 223, (37) * 24

Получаем очевидное решение для других трёх неизвестных переменных:

x 222= 9000/3 = 3000; x 221= 3000; x 223= 3000.

Наконец, рассмотрим равенства (12) * 9, (39) * 26 и (40) * 27:

f 33= x 331+ x 332+ x 333= 12000, (12) * 9

x 331 = x 333, (39) * 26

x 332 = x 333. (40) * 27

Получаем очевидное решение для последних трёх неизвестных переменных:

x 333= 12000/3 = 4000; x 331= 4000; x 332= 4000

Таким образом для получения искомого решения оказалось достаточно лишь девяти вышеприведённых уравнений, а именно: (4) * 1, (32) * 19, (33) * 20, (8) * 5, (35) * 22, (37) * 24, (12) * 9, (39) * 26 и (40) * 27. Как ранее было показано прочие переменные этой системы линейных уравнений в данном численном примере равны нулю.