Александр Бакулин - Гравитация и эфир

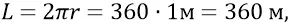
откуда расстояние r (4–10),

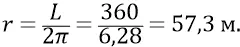
Если мы теперь на этой площадке разместим (одна к одной) конструкции квантов-частиц (они имеют размеры такие же как у электрона – 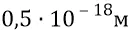), то можем вычислить количество квантов-частиц, с их плотностью распределения на площадке – «одна к одной», которые будут постоянно собираться из эфира по конусу с раскрывом в 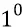, параллельно к плоскости поляризации кварка 4. При любых вращениях кварка 4 (при вращениях – как вокруг собственной оси, так и по хордовой орбите внутри нуклона, эту плоскость можно считать как бы «приклеенной» к плоскости поляризации кварка. То есть она будет быстро вращаться вместе с вращением кварка, собирая кванты в конусе каждый раз с того направления, куда в данное мгновение будет «смотреть» кварк 4.

Итак, на площадке одного квадратного метра разместится следующее количество квантов эфира:

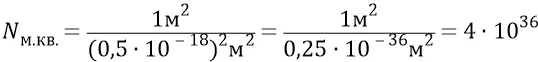квантов эфира.

Эта цифра пока ещё ни о чём не говорит, то есть никак пока не говорит о возможной реальной плотности квантов эфира, размещаемых в реальном вакууме на площади квадратного метра. Она, эта цифра, должна быть в результате той, которую мы «сошьём» с энергией глюона, излучаемого квантом 4 из собираемых им квантов конуса. Если на площадке квадратного метра расположен единичный квант (из их количества там 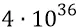штук), то это не значит, что этот квант «сейчас» полетит точно на кварк 4. Квант площадки, как реальный квант-частица эфира, оказавшийся в данное мгновение в пределах этой площадки, может лететь в левую сторону от неё – в направление кварка – по любому лучу левой полусферы радиуса r. Поэтому сейчас нам придётся подсчитать вероятность того события, когда квант площадки, двигаясь справа-налево, попадёт точно на размер кварка.

Площадь левой полусферы 8–4–9 с её осью 4–10 (формула площади полной сферы S=4π :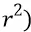

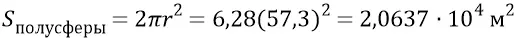
Количество частиц, которые можно разместить на этой полусфере «одна к одной»:

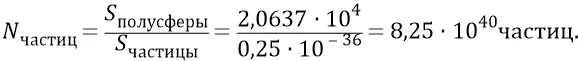
Итак, если предположить, для начала, что любой из квантов эфира площадки S должен попадать точно по центру масс кварка 4, то вероятность такого события для каждого кванта эфира площадки будет:

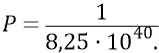
Но, кроме того, для эффективного взаимодействия кванта и кварка 4, их поляризации должны совпадать (в данном случае их поляризации должны быть «вертикальными»). Это уменьшает общую вероятность эффективного взаимодействия кванта и кварка вдвое. И, кроме того, из всех квантов площадки S нам годятся только те кванты-частицы, которые совпадают с данным кварком (4) по знаку заряда этого кварка. Если этот кварк, например, – электрон, то мы отбираем с площадки S только «отрицательные» кванты, которые, взаимодействуя с электроном, излучатся «из него» квантами «отрицательного» поля электрона. Поэтому вероятность нужных нам квантов площадки S придётся ещё раз ополовинеть.

Но ещё и кроме того: любой квант площадки S обязан подлететь к кванту 4 «кольцо к кольцу» по своей пространственной фазе. Причём они должны встретится именно соответствующими сторонами из колец (конструктивные вопросы эффективных взаимодействий электромагнитных квантов на их преонном уровне, в данном издании нашей книги мы пока не рассматриваем; но заранее утверждаем при этом, что, например, электрон только тогда может эффективно провзаимодействовать с налетающим на него «отрицательным» квантом, когда этот квант налетает только одной определённой стороной своего кольца; если же он налетит, хотя и точно по цели, но другой стороной кольца, то из такого кванта не получится поляэлектрона, но он для последнего будет представлять обычный эфирный квант, никак не взаимодействующий с электроном). Итак, по этому признаку нам придётся уменьшить вероятность отбора нужных квантов с площадки S для поля кварка 3 ещё в 360 раз. Итого вероятность отбора квантов для кварка 4 определится величиной:

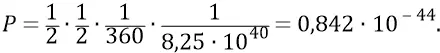
Обращаем внимание, что при вычислении данной вероятности мы не учитываем возможное уменьшение последней цифры ещё в 360 раз (за счёт распределения возможного углового положения самого кольца кварка 4), поскольку это его вертикальное положение у нас изначально нормировано. То есть при любом повороте кольца кварка 4 от вертикали, вместе с ним будет смещаться площадка S по периметру L (мы об этом уже говорили).

Итак, уже сейчас – на этом этапе, мы можем в первом приближении оценить плотность распределения квантов реального эфира на площадке одного квадратного метра, которая должна быть такой, что умноженная на полученную вероятность, должна дать значение не менее единицы:

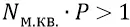
И поскольку природа вещей не любит излишеств, то выберем значение N равным:

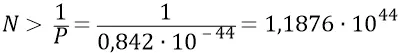
Однако (для ровного счёта) мы округлим цифру количества частиц на площадке квадратного метра в меньшую сторону:

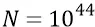частиц

на площадке квадратного метра, со сторонами из количества частиц по каждой стороне квадрата (частиц с собственными размерами 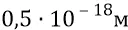), уплотнённых по расстояниям между их центрами масс – «один к одному» – 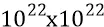частиц.

Шаг центров масс частиц по стороне квадрата 1 м:

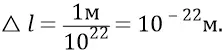
То есть получили уплотнение частиц в эфире настолько сильным, что на размере-диаметре одной частицы ( 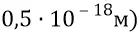размещаются