Яков Перельман - Головоломки и развлечения
- Название:Головоломки и развлечения
- Автор:
- Жанр:
- Издательство:АСТ
- Год:2020
- Город:Москва
- ISBN:978-5-17-122300-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Яков Перельман - Головоломки и развлечения краткое содержание
Для среднего школьного возраста.
Головоломки и развлечения - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Нетрудно, например, вставив плюс и минус шесть раз, получить 100 таким путем:
12 + 3–4 + 5 + 67 + 8 + 9 = 100.
Если хотите вставить плюс и минус только четыре раза, вы тоже можете получить 100:
123 + 4–5 + 67–89 = 100.
Попробуйте, однако, получить 100, пользуясь знаками плюс и минус всего только три раза.
Это гораздо труднее. И все же вполне возможно — надо только терпеливо поискать.
Пятью двойками
Можно ли пятью двойками выразить число 28?
Четырьмя двойками
Эта задача замысловатее предыдущих. Надо четырьмя двойками выразить число 111. Возможно ли это?
Число 37
Напишите подобным же образом число 37, пользуясь только пятью тройками и знаками действий.
Деление на 11
Напишите какое-нибудь девятизначное число, в котором нет повторяющихся цифр (все цифры разные) и которое делится без остатка на 11.
Напишите наибольшее из таких чисел.
Напишите наименьшее из таких чисел.
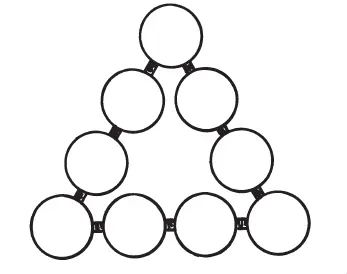
Числовой треугольник
В кружках этого треугольника расставьте все девять значащих цифр так, чтобы сумма их на каждой стороне составляла 20.
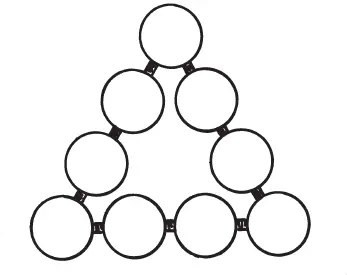
Еще числовой треугольник
Все значащие цифры разместить в кружках того же треугольника так, чтобы сумма их на каждой стороне равнялась 17.
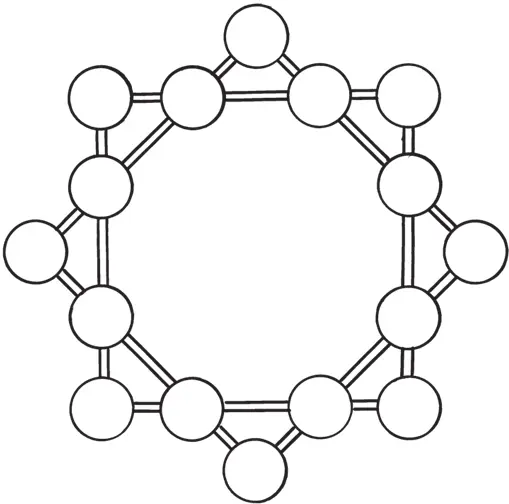
Восьмиконечная звезда
Числа от 1 до 16 надо расставить в точках пересечения линий фигуры, изображенной на рисунке, так, чтобы сумма чисел на стороне каждого квадрата была 34 и сумма их на вершинах каждого квадрата также составляла 34.
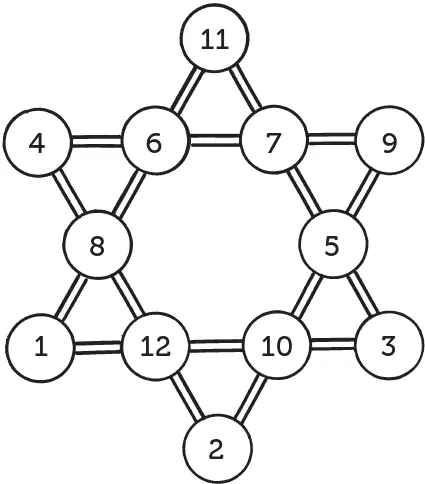
Магическая звезда
Шестиконечная числовая звезда, изображенная на рисунке, обладает «магическим» свойством: все шесть рядов чисел имеют одну и ту же сумму:
4 + 6 + 7 + 9 = 26
4 + 8 + 12 + 2 = 26
9 + 5 + 10 + 2 = 26
11 + 6 + 8 + 1 = 26
11 + 7 + 5 + 3 = 26
1 + 12 + 10 + 3 = 26.
Но сумма чисел, расположенных на вершинах звезды, другая:
4 + 11 + 9 + 3 + 2 + 1 = 30.
Не удастся ли вам усовершенствовать эту звезду, расставив числа в кружках так, чтобы не только прямые ряды давали одинаковые суммы (26), но чтобы ту же сумму (26) составляли числа на вершинах звезды?
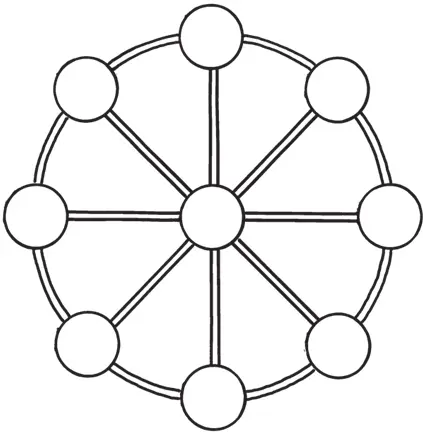
Числовое колесо
Цифры от 1 до 9 надо разместить в этой фигуре так, чтобы одна цифра была в центре круга, прочие — у концов каждого диаметра и чтобы сумма трех цифр каждого ряда составляла 15.
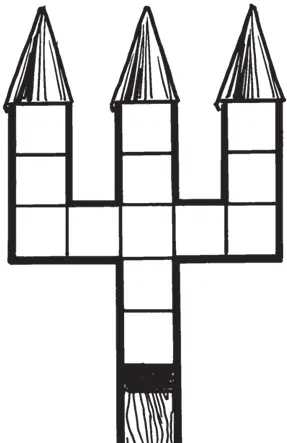
Трезубец
В клетках изображенного здесь трезубца нужно расставить числа от 1 до 13 так, чтобы сумма цифр в каждом из трех вертикальных рядов (I, II, III) и в одном горизонтальном (IV) была одинакова.
Попробуйте это сделать.
Ответы
Из семи цифр
Задача имеет не одно, а три разных решения. Вот они:
123 + 4–5 — 67 = 55;
1 — 2–3 — 4 + 56 + 7 = 55
12 — 3 + 45 — 6 + 7 = 55.
Девять цифр
Вот каким способом можете вы получить 100 из разряда девяти цифр и трех знаков плюс и минус:
123 — 45–67 + 89 = 100.
Это — единственное решение; никакое другое сочетание девяти цифр и знаков плюс и минус, употребленных три раза, не дает в результате 100.
Достигнуть того же результата, употребив знаки сложения и вычитания менее трех раз, невозможно.
Пятью двойками
22 + 2 + 2 + 2 = 28.
Четырьмя двойками
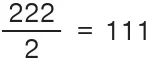
Число 37
Решений имеется два:
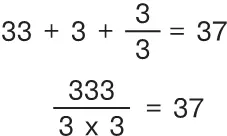
Деление на 11
Чтобы решить эту задачу, надо знать признак делимости на 11. Число делится на 11, если разность между суммой цифр, стоящих на четных местах, и сумма цифр, стоящих на нечетных местах, делится на 11 или равна нулю.
Испытаем, для примера, число 23 658 904.
Сумма цифр, стоящих на четных местах:
3 + 5 + 9 + 4 = 21;
сумма цифр, стоящих на нечетных местах:
2 + 6 + 8 + 0 = 16.
Разность их (надо вычитать из большего меньшее) равна:
21 — 16 = 5.
Эта разность (5) не делится на 11; значит, и взятое число не делится без остатка на 11.
Испытаем другое число — 7 344 535:
3 + 4 + 3 = 10;
7 + 4 + 5 + 5 = 21;
21 — 10 = 11.
Так как 11 делится на 11, то испытуемое число кратно 11.
Теперь легко сообразить, в каком порядке надо писать девять цифр, чтобы получилось число, кратное 11 и удовлетворяющее требованиям задачи.
Вот пример: 352 049 786.
Испытаем:
3 + 2 + 4 + 7 + 6 = 22;
5 + 0 + 9 + 8 = 22.
Разность 22–22 = 0; значит, написанное нами число кратно 11.
Наибольшее из всех таких чисел есть: 987 652 413.
Наименьшее: 102 347 586.
Числовой треугольник
Решение показано на рисунке. Средние цифры каждого ряда можно переставить и получить, таким образом, еще ряд решений.
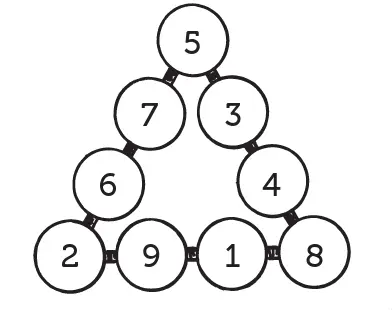
Еще числовой треугольник
Решение этой головоломки можно увидеть на рисунке. Средние цифры каждого ряда можно переставить и получить, таким образом, еще ряд решений.
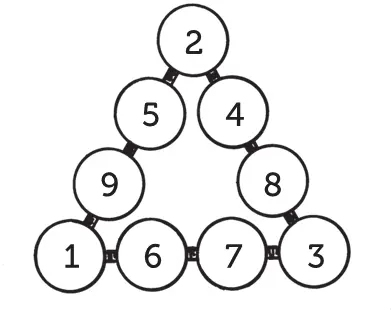
Восьмиконечная звезда
Решение можно увидеть на рисунке:
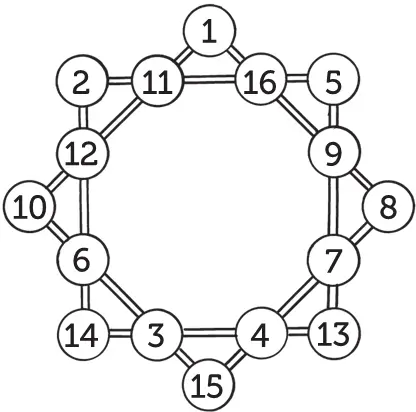
Магическая звезда
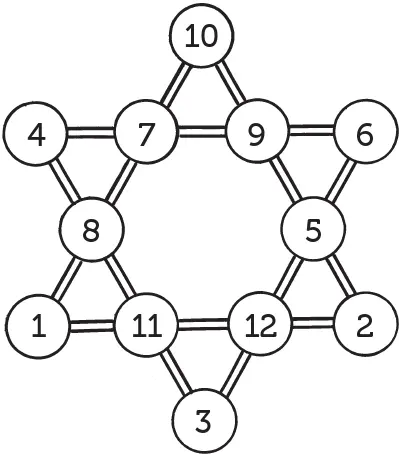
Чтобы облегчить себе отыскание требуемого расположения чисел, будем руководствоваться следующими соображениями.
Сумма чисел на концах искомой звезды равна 26; сумма же всех чисел звезды — 68. Значит, сумма чисел внутреннего шестиугольника равна 78–26 = 52.
Рассмотрим затем один из больших треугольников. Сумма чисел каждой его стороны равна 26; сложим числа всех трех сторон — получим 26 × 3 = 78, причем каждое из чисел, стоящих на углах, входит дважды. А так как сумма чисел трех внутренних пар (то есть внутреннего шестиугольника) должна, мы знаем, равняться 52, то удвоенная сумма чисел на вершинах каждого треугольника равна 78–52 = 26; однократная же сумма равна 13.
Читать дальшеИнтервал:
Закладка:










