Яков Перельман - Головоломки и развлечения
- Название:Головоломки и развлечения
- Автор:
- Жанр:
- Издательство:АСТ
- Год:2020
- Город:Москва
- ISBN:978-5-17-122300-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Яков Перельман - Головоломки и развлечения краткое содержание
Для среднего школьного возраста.
Головоломки и развлечения - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Два четырехугольника
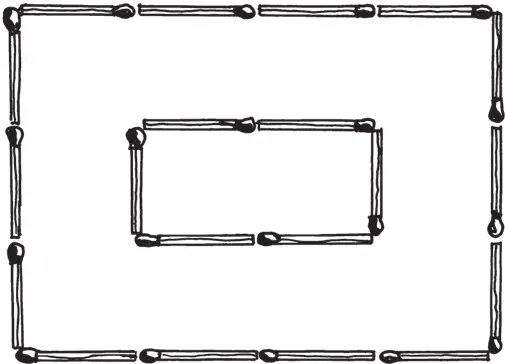
На рисунке изображен четырехугольник из шести спичек, площадь которого вдвое больше площади квадрата со стороной, равной одной спичке. Так как длина спички вам известна — 5 см, — то вы легко определите площадь вашего четырехугольника в сантиметрах: 5 × 10 = 50 кв. см. Задача состоит в следующем: не изменяя длины обвода этого четырехугольника, изменить форму его так, чтобы площадь уменьшалась вдвое, то есть равнялась 25 см. Как это сделать?
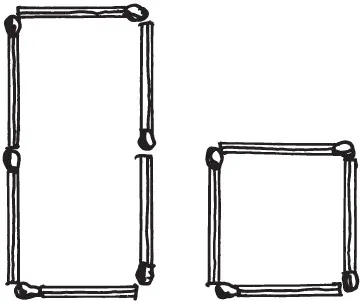
Пусть читатель обратит внимание на то, что речь идет о составлении четырехугольной фигуры (а не непременно прямоугольной): углы новой фигуры не обязательно должны быть прямые.
Надо из шести спичек сложить параллелограмм так, чтобы его высота равнялась одной спичке. Такой параллелограмм, имеющий одинаковые основание и высоту с квадратом, должен иметь и одинаковую с ним площадь.
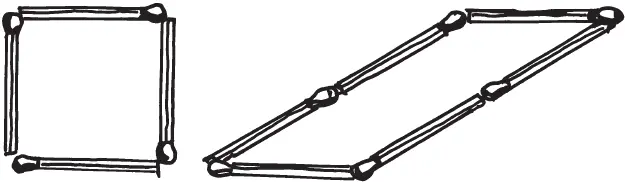
Что больше?
Из шести спичек сложены прямоугольник и равносторонний треугольник. Обводы этих фигур, конечно, одинаковы. А у какой больше площадь?

Чтобы решить эту задачу, надо знать, как вычисляется площадь треугольника: умножают длину основания на высоту и полученное произведение делят пополам, или — что то же самое — умножают половину основания на высоту. В нашем треугольнике половина основания равна одной спичке, то есть основанию прямоугольника. Если бы высоты этих фигур были одинаковы, то обе фигуры имели бы равные площади. Но легко видеть, что высота треугольника меньше двух спичек, то есть меньше высоты прямоугольника. Значит, и площадь треугольника меньше площади прямоугольника.
Фигура с наибольшей площадью
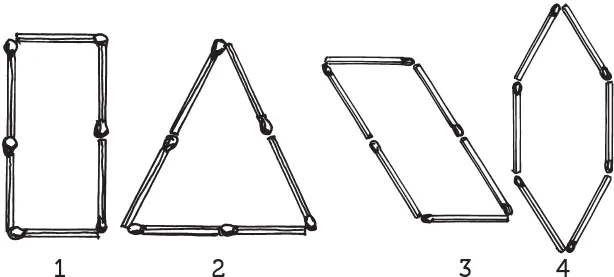
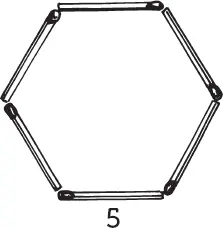
Сейчас мы составили из шести спичек прямоугольник и равносторонний треугольник. Но из того же числа спичек можно составить еще и другие фигуры, имеющие одинаковый обвод. Некоторые из них изображены на рисунке ниже.
Площади всех этих фигур различны. Спрашивается, у какой же из них площадь наибольшая?
Мы уже знаем, что площадь фигуры 1 больше площади фигуры 2. Легко сообразить, что она больше также и площади фигуры 3 (сравните их высоты!). Остается, следовательно, сравнить по величине площади фигур 1, 4 и 5. Мы можем рассматривать все три фигуры как шестиугольники с равными сторонами (у фигуры 1 два угла выпрямлены). В курсах геометрии доказывается, что из всех многоугольников с одинаковым числом сторон и одинаковым обводом наибольшую площадь имеет многоугольник правильный, то есть такой, у которого равны не только стороны, но и углы. Этому условию удовлетворяет фигура 5; она, следовательно, и имеет наибольшую площадь, какую можно ограничить шестью спичками.
Мост из двух спичек
На рисунке вы видите остров, окруженный каналом. Ширина канала как раз равна длине одной спички, так что перебросить мостик через канал с помощью одной спички нельзя: невозможно опереться концами о берега канала.
Не удастся ли вам перекинуть мост через канаву с помощью двух спичек? Помните, однако, что склеивать или связывать эти две спички не полагается.
Решение этой задачи основано на том, что длина линии, соединяющей противоположные углы квадрата (так называемая диагональ), меньше длины 1,5 спичек (рисунок а ).
Зная это, мы можем построить требуемый мост так, как показано на рисунке б, то есть одну спичку кладем в положение 5–6, а другую — в положение 7–4. Расстояние 2–7, очевидно, равно расстоянию 5–7; расстояние 2–4, то есть диагональ квадрата, меньше длины 1,5 спичек; а так как расстояние 2–7 равно половине спички, то пролет 7–4 короче длины спички. Отсюда и вытекает возможность сооружения нашего моста.
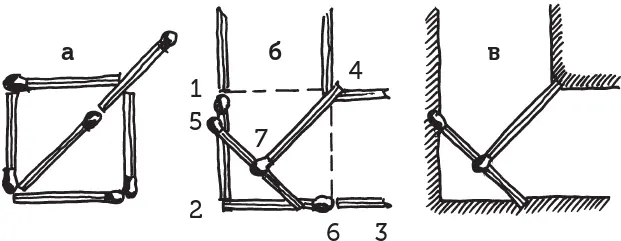
Задача эта может оказаться и практически полезной в том случае, когда, имея даже две одинаковые жерди, нужно перебросить (не связывая их между собой) мост через канаву, ширина которой как раз равна или даже чуть больше длины одинаковой жерди. Возможно это, впрочем, только в том месте канавы, где она поворачивает под прямым углом (рисунок в ).
Витрина магазина
В витринах магазина нередко выставляются ради рекламы огромные спичечные коробки, по фасону совершенно подобные обыкновенным; а внутри коробки видны столь же чудовищные спички. Предположим, что такой коробок в 10 раз длиннее обыкновенного. Спрашивается:
1) Сколько весит одна исполинская спичка, принимая вес обыкновенной спички в 1/10 г?
2) Сколько спичек обыкновенного размера мог бы вместить один коробок-великан?
Ответ, что спичка весит 1/10 × 10, то есть всего 1 г, конечно, явно несообразен: ведь это чуть не настоящее полено — правда, всего в 2 см толщины, зато в 1/2 м длины!
Так же несообразно допустить, что в огромном коробке всего вдесятеро больше спичек, чем в обыкновенном, то есть столько, сколько в 10 коробках. 10 выложенных в ряд коробков не похожи на тот внушительный ящик, который выставлен в витрине.
Каковы же правильные ответы?
Огромная спичка не только в 10 раз длиннее обыкновенной, но и в 10 раз толще и шире; следовательно, она превышает обыкновенную спичку по объему в 10 × 10 × 10, то есть в 1000 раз. Отсюда определяем вес ее: 1/10 × 1000 = 100 г.
Точно так же коробок-великан вместительнее обыкновенного в 1000 раз, и, значит, в него может войти около 50 тысяч обыкновенных спичек.

Задачи из путешествий Гулливера

Самые удивительные страницы в «Путешествиях Гулливера по многим отдаленным странам» — без сомнения, те, где описаны его необычайные приключения в стране крошечных лилипутов и в стране великанов «бробдиньягов». В стране лилипутов размеры — высота, ширина, толщина — всех людей, животных, растений и вещей были в 12 раз меньше, чем у нас. В стране великанов, наоборот, — в 12 раз больше. Почему автор «Путешествий» избрал именно число 12, легко понять, если вспомнить, что это как раз отношение фута к дюйму (автор «Путешествий» — англичанин). В 12 раз меньше, в 12 раз больше — как будто не очень значительное уменьшение или увеличение. Однако отличие природы и жизни в этих фантастических странах от тех, к каким мы привыкли, оказалось поразительным. Зачастую различие это настолько озадачивает своей неожиданностью, что дает материал для головоломной задачи. Десяток подобных головоломок мы и хотим здесь предложить читателям.
Читать дальшеИнтервал:
Закладка:










