Яков Перельман - Головоломки и развлечения

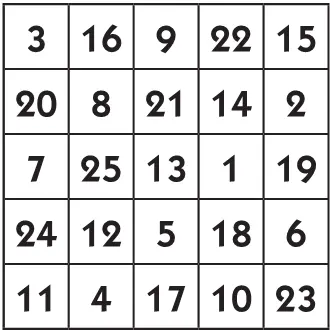
Обоснование этого простого приема довольно сложно; читатели могут удостовериться на практике, что способ правилен.

Составив один магический квадрат из 25 клеток, вы путем поворотов и отражений можете получить его видоизменения.

Способ Баше, или, как его иначе называют, «способ террас», — не единственный для составления квадратов с нечетным числом клеток. Из других существующих способов сравнительно несложен весьма древний прием, придуманный, как полагают, в Индии еще до начала нашего летоисчисления. Его можно изложить кратко в шести правилах. Внимательно прочтите все правила, а затем проследите их применение на примере магического квадрата из 49 клеток:

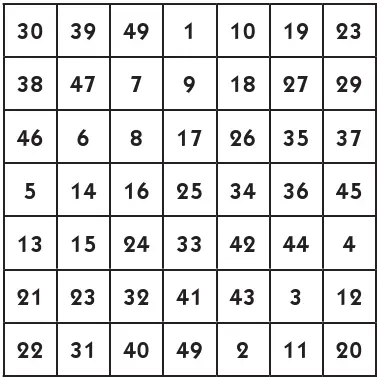
1. В середине верхней строки пишут 1, а в самом низу среднего справа столбца — 2.

2. Следующие числа пишут по порядку в диагональном направлении вправо и вверх.

3. Дойдя до правого края квадрата, переходят к крайней левой клетке ближайшей вышележащей строки.

4. Дойдя до верхнего края квадрата, переходят к самой нижней клетке соседнего справа столбца.

Примечание. Дойдя до правой верхней угловой клетки, переходят к левой нижней.

5. Дойдя до уже занятой клетки, переходят к клетке, лежащей непосредственно под последней заполненной клеткой.

6. Если последняя заполненная клетка находится в нижнем ряду квадрата, переходят к самой верхней клетке в том же столбце.

Руководствуясь этими правилами, можно быстро составлять магические квадраты с любым нечетным числом клеток.

Если число клеток квадрата не делится на 3, можно начинать составление магического квадрата не по правилу 1, а по другому правилу.

Единицу можно написать в любой клетке диагонального ряда, идущего от средней клетки крайнего левого столбца к средней клетке самой верхней строки квадрата. Все последующие числа вписываются согласно правилам 2–5.

Это дает возможность составить по индийскому способу не один, а несколько квадратов. Как например даем следующий магический квадрат из 49 клеток.

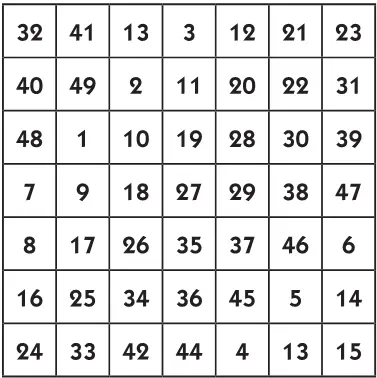
Упражнение. Составьте по индийскому способу несколько магических квадратов из 25 и из 45 клеток. Из полученных квадратов составьте еще несколько с помощью повторов и отражений.

Для составления магических квадратов с четным числом клеток еще не найдено общего и удобного правила. Сравнительно простой прием существует лишь для таких четных квадратов, число клеток которых делится без остатка на 16; число клеток в стороне этих квадратов кратно 4, то есть сторона их состоит из 4, из 8, из 12 и т. д. клеток.

Условимся, какие клетки мы будем называть «противолежащими» друг другу. На рисунке ниже показаны для примера две пары противолежащих клеток: одна пара обозначена крестиками, другая — кружочками.

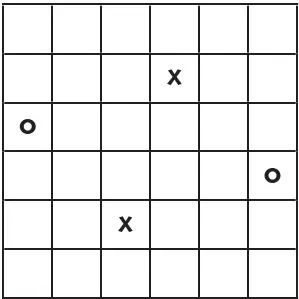
Мы видим, что если клетка находится во втором сверху ряду на четвертом слева месте, то противолежащая ей клетка находится во втором снизу ряжу на четвертом справа месте. (Читателю полезно поупражняться в нахождении еще нескольких пар противолежащих клеток.) Заметим, что для клеток, взятых в диагональном ряду, противолежащие расположены на этой же диагонали.

Способ составления квадратов с указанным числом клеток в стороне объясним на примере квадрата из 8 × 8 клеток. Начинают с того, что вписывают в клетки по порядку все числа от 1 до 64.

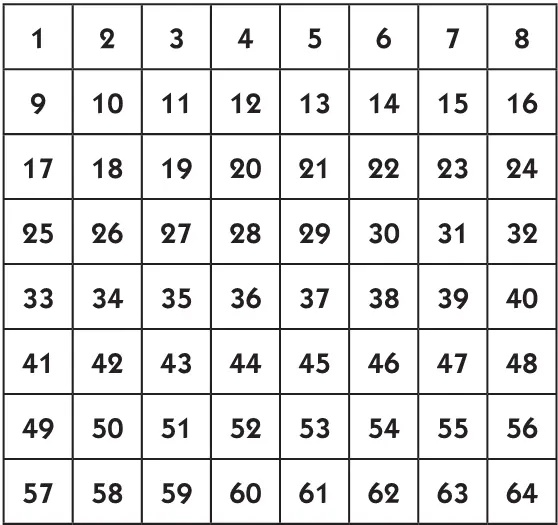
В полученном квадрате диагональные ряды дают одинаковую сумму — 260, как раз такую, какая и должна быть в магическом квадрате из 8 × 8 клеток. (Проверьте это!) Но строки и столбцы этого квадрата имеют другие суммы.

Так, первая верхняя строка дает в сумме всего 36, то есть на 224 меньше, чем требуется (260 — 36); восьмая, самая нижняя, строка дает в сумме 484, то есть на 224 больше, чем требуется (484–260). Замечая, что каждое число восьмой строки на 56 больше находящегося над ним числа первой строки и это 224 = 4 × 56, приходим к выводу, что можно уравнять суммы этих строк, если половину чисел первой строки обменять местами с числами 57, 58, 59, 60.

Сказанное о первой и восьмой строках верно так же для строк второй и седьмой, третьей и шестой, вообще для каждой пары строк, равноотстающих от крайних. Производя обмен чисел во всех строках, получим квадрат с одинаковыми суммами строк.

Необходимо, однако, чтобы и столбцы давали ту же сумму. При первоначальном расположении чисел мы могли бы достигнуть этого путем такого же обмена чисел, какой мы произвели сейчас с числами строк. Но теперь, после перестановок в строках, дело осложнилось. Чтобы быстро отыскать числа, подлежащие обмену, существует следующий прием, которым можно пользоваться с самого начала: вместо двояких перестановок — в строках и в столбцах — обменивают местами те числа, которые противолежат друг другу. Одного этого правила все же недостаточно — ведь мы установили, что обмену подлежат не все числа ряда, а только половина; остальные числа остаются на прежних местах. Какие же из противолежащих пар надо обменивать?

На этот вопрос отвечают следующие четыре правила:

1. Надо магический квадрат разделить на четыре квадрата, как показано на рисунке:

2. В левом верхнем квадрате отметить крестиками половину всех клеток так, чтобы в каждом столбце и в каждой строке этого квадрата была отмечена ровно половина входящих в них клеток. Это можно сделать различными способами — например, так, как показано на приведенной выше фигуре.

3. В правом верхнем квадрате отметить крестиками клетки, симметричные тем, которые были отмечены в левом верхнем квад-рате.

4. Теперь остается числа, находящиеся в отмеченных клетках, поменять местами с числами, находящимися в противолежащих клетках.

В результате всех проделанных перестановок получается магический квадрат из 64 клеток, который здесь приведен:

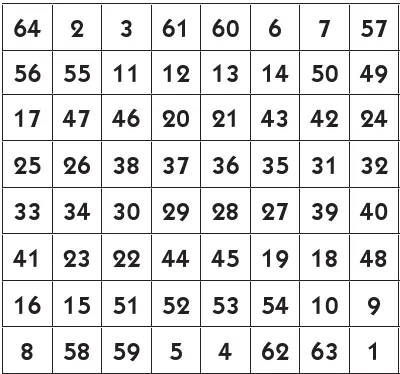
Мы могли бы, однако, и многими другими способами отметить клетки в левом верхнем квадрате, причем правило 2 было бы соблюдено.