Яков Перельман - Головоломки и развлечения
- Название:Головоломки и развлечения
- Автор:
- Жанр:
- Издательство:АСТ
- Год:2020
- Город:Москва
- ISBN:978-5-17-122300-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Яков Перельман - Головоломки и развлечения краткое содержание
Для среднего школьного возраста.
Головоломки и развлечения - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Это можно сделать, например, так, как показано на помещенном здесь рисунке.
Читатель несомненно сам найдет еще очень много способов расстановки крестиков в клетках левого верхнего квадрата.
Пользуясь затем правилами 3 и 4, можно будет получить еще несколько магических квадратов из 64 клеток.
Таким же способом можно построить магические квадраты, состоящие из 12 × 12, 16 × 16 и так далее клеток.
Предлагаем читателю самостоятельно проделать это.
Откуда магические квадраты получили свое название
Первое упоминание о магическом квадрате встречается в древнейшей китайской книге, относящейся к эпохе за 4000–5000 лет до нашего времени.
Глубже были знакомы с магическими квадратами в древней Индии. Из Индии увлечение магическими квадратами перешло к арабам, которые приписывали этим числовым сочетаниям таинственные свойства.
В Западной Европе в Средние века магические квадраты были достоянием представителей мнимых наук — алхимии и астрологии. От старинных суеверных представлений эти числовые квадраты и получили свое необычное в математике название — «магические», то есть волшебные. Астрологи и алхимики верили, что дощечка с изображенным на ней магическим квадратом способна отвратить беду от человека, который носит на себе такой талисман.
Составление магических квадратов не является только забавой. Теорию их разрабатывали многие выдающиеся математики.
Она находит применение в некоторых важных математических вопросах. Так, например, имеется способ решения систем уравнений со многими неизвестными, который использует выводы теории магических квадратов.
Задачи о транспорте

Перелет
Самолет покрывает расстояние от города А до города В за 1 час 20 минут. Однако обратный перелет он совершает в 80 минут.
Как вы это объясните?
Два паровоза
Вам случалось, наверное, видеть, как поезд везут два паровоза: один — впереди состава, другой — сзади. Но думали ли вы о том, что при этом происходит со сцепкой вагонов с буферами? Передний паровоз увлекает за собой вагоны лишь тогда, когда их сцепка натянута; но при этом буфера не соприкасаются, и задний паровоз не может толкать вагоны. Наоборот, когда задний паровоз толкает состав, буфера напирают друг на друга, сцепка же не натянута, а потому работа переднего паровоза бесполезна.
Выходит, что оба паровоза не могут одновременно двигать поезд: с пользой работает либо один, либо другой паровоз.
Для чего же прицепляют два паровоза?
Скорость поезда
Вы сидите в вагоне поезда и желаете знать, с какой скоростью он мчится.
Можете ли вы определить это по стуку колес?
Два поезда
Два поезда вышли одновременно с двух станций навстречу друг другу. Первый достиг станции назначения спустя час после их встречи, второй — спустя 2 часа 15 минут после встречи.
Во сколько раз скорость одного поезда больше скорости другого?
Задача допускает устное решение.
Как поезд трогается с места?
Вы заметили, вероятно, что перед тем, как двинуть поезд вперед, машинист нередко подает весь состав назад.
Для чего это делается?
Состязание
Две парусные лодки участвуют в состязании: требуется пройти 24 км туда и обратно в кратчайшее время. Первая лодка прошла весь путь с равномерной скоростью 20 км в час; вторая двигалась туда со скоростью 16 км в час, а обратно — со скоростью 24 км в час.
Победила на состязании первая лодка, хотя, казалось бы, вторая должна была в одном направлении отстать от первой ровно на столько же, на сколько она опережала ее на обратном пути, и, следовательно, прийти одновременно с первой.
Почему же она опоздала?
От Энска до Иксограда
Плывя по течению, пароход делает 20 км в час; плывя против течения — всего 15 км в час. Чтобы пройти от пристани города Энска до пристани Иксограда, он употребляет на 5 часов меньше, чем на обратный путь.
Как велико расстояние между этими городами?
Ответы
Перелет
В этой задаче нечего объяснять: самолет совершает перелет в обоих направлениях в одинаковое время, потому что 80 минут = 1 часу 20 минутам.
Задача рассчитана на невнимательность читателя, который может подумать, что между 1 часом 20 минутами и 80 минутами есть разница. Как ни странно, но людей, попадающихся на этот крючок, оказывается немало, притом среди привыкших делать расчеты их больше, чем среди малоопытных вычислителей. Причина кроется в привычке к десятичной системе мер и денежных единиц. Видя обозначение «1 час 20 минут» и рядом с ним «80 минут», мы невольно оцениваем различие между ними, как разницу между 1 рублем 20 копейками и 80 копейками. На эту психологическую ошибку и рассчитана задача.
Два паровоза
Головоломный вопрос решается очень просто. Передний паровоз тянет не весь состав, а только часть его, примерно половину вагонов. Остальные вагоны подталкиваются задним паровозом. У первой части состава сцепка вагонов натянута, у остальной она свободна, и вагоны упираются буфер в буфер.
Скорость поезда
Вы заметили, конечно, что при езде в вагоне ощущаются все время мерные толчки; никакие рессоры не могут сделать их неощутимыми. Толчки эти происходят оттого, что колеса слегка сотрясаются в местах соединения двух рельсов и толчок передается всему вагону.
Эти-то неприятные толчки, довольно разрушительно действующие на вагоны и рельсы, можно использовать для определения скорости поезда. Стоит лишь сосчитать, сколько толчков в минуту испытывает вагон, чтобы узнать, сколько рельсов пробежал поезд. Остается умножить это число на длину каждого рельса, — и вы получите расстояние, проходимое поездом в минуту.
Обычная длина рельса — около 15 м (выйдя на станции из вагона, вы можете, измеряя рельсы шагами, узнать их длину; каждые семь шагов можно принять за 5 м). Сосчитав с часами в руках число толчков в минуту, умножьте это число на 15, затем на 60 и делите на 1000 — получится число километров, пробегаемое поездом в час:
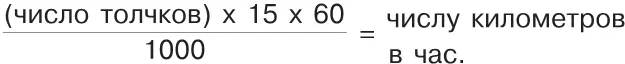
Два поезда
Более быстрый поезд прошел до точки встречи путь во столько же раз длиннее пути медленного поезда, во сколько раз скорость быстрого поезда превышает скорость медленного. После встречи быстрому поезду оставалось пройти до станции путь, пройденный до встречи медленным поездом, и наоборот.
Читать дальшеИнтервал:
Закладка:










