Александр Киселев - Математика шахматной доски

Ясно, что на мономино шахматная доска разбивается достаточно легко. Не вызывает особенных проблем и её разбиение на домино.

Рисунок 4. Разбиение на мономино

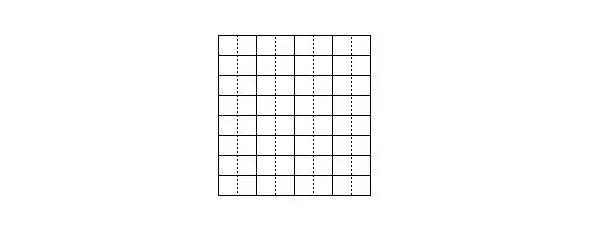
Рисунок 5. Разбиение на домино

Попытка разбить на прямые тримино приводит к тому, что остаётся одна клетка, не входящая ни в одну фигурку. Младшие школьники обычно либо в растерянности (им в принципе непривычно, что на вопрос «можно ли» бывает отрицательный ответ), либо говорят, что разрезать невозможно, потому что у них осталась одна лишняя клетка.

Школьник постарше, знакомый с понятием делимости, сразу формулирует это иначе: доску нельзя разрезать на тримино (хоть на прямые, хоть на угловые), потому что её площадь не делится на 3 (не делится без остатка , как принято называть это явление в школе 2 2 По поводу понятия делимости смотрите Приложение 3. ). Интересно, что на резонный вопрос «А почему она должна делиться?» некоторые из них ответить не могут, то есть это наблюдение настолько интуитивно очевидное, что далеко не всегда ребёнок задумывается над его причинами.

Итак, если шахматную доску (а, вообще говоря, любую клетчатую фигуру с целой площадью) можно разбить на полимино определённого вида (а, вообще говоря, на любые фигуры с целой площадью), то и площадь доски (большей фигуры) обязательно должна делиться на площадь этого полимино (меньшей фигуры). Более того, частное при этом делении равно количеству фигурок, получающихся при разрезании (это наблюдение пригодится нам в дальнейшем).

Условие делимости площадей является необходимым, то есть если площадь доски не делится на площадь маленьких фигурок, то разрезать точно не удастся. Обратное неверно!

Но для тримино всё работает идеально в нужную сторону: площадь шахматной доски (64 клетки) не делится на площадь тримино (3 клетки), поэтому её невозможно разрезать ни на прямые, ни на угловые тримино.

Так как 64 делится на 4, то никаких очевидных проблем с разрезанием доски на тетрамино не предвидится. Действительно, на прямые, квадратные, L- и T- тетрамино её разрезать можно.

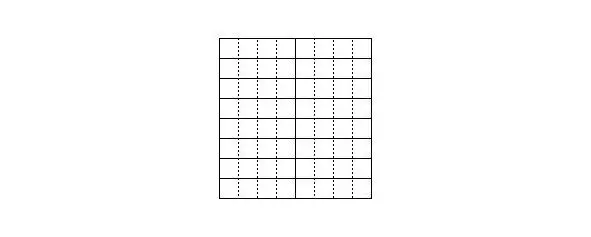
Рисунок 6. Разбиение на прямые тетрамино

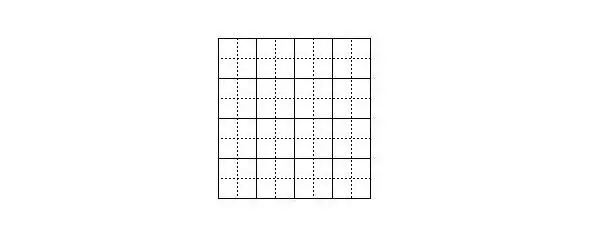
Рисунок 7. Разбиение на квадратные тетрамино

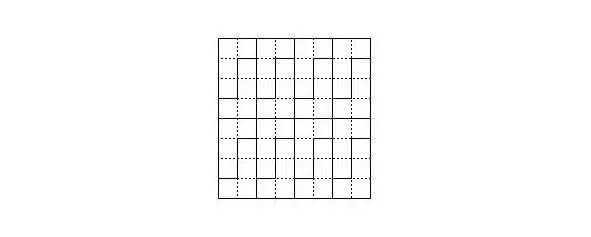
Рисунок 8. Разбиение на L-тетрамино

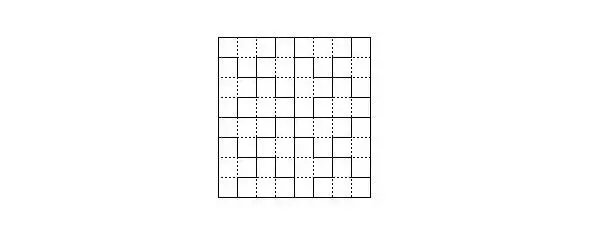
Рисунок 9. Разбиение на T-тетрамино

С косыми тетрамино ситуация оказывается интереснее. Иногда школьники, не поверившие в то, что необходимого условия может оказаться недостаточно, просто говорят, что площадь делится на 64, поэтому разрезать можно. На просьбу показать пример отвечают, что у них не получилось.

На самом деле разрезать шахматную доску (как и любой другой прямоугольник) на косые тетрамино нельзя. Классическое доказательство этого факта такое: предположим, что у нас получилось, тогда каждая клетка доски входит в какое-то косое тетрамино. Рассмотрим угловую клетку, у неё есть всего два варианта, какой тетраминошкой она покрыта (на самом деле эти варианты одинаковы с точностью до поворота доски).

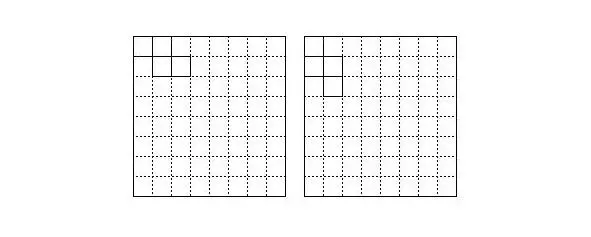
Рисунок 10. Варианты покрытия угловой клетки косым тетрамино

Тогда третья от угла клетка покрыта однозначно, тогда и пятая от угла покрыта однозначно, а для покрытия седьмой от угла уже не остаётся никакой возможности.

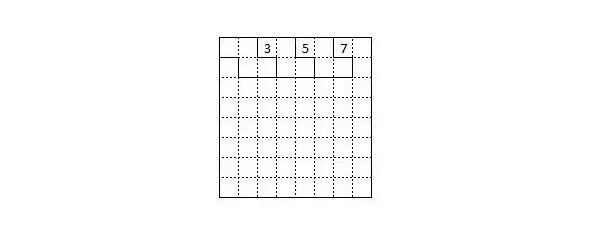
Рисунок 11. Покрытие стороны косыми тетрамино

Такое же рассуждение можно провести и для прямоугольника любого другого размера.

Получилась важная вещь: необходимого условия вовсе не достаточно, чтобы утверждать, что разрезание возможно. Эту информацию можно донести до школьника и на более очевидном примере (я особенно люблю полоску 1×64), но иногда школьнику кажется, что если доска будет достаточно широкой, чтобы хотя бы одно полимино на неё поместилось, то никаких проблем с разрезанием он не встретит. Шахматная доска лучше подходит для развенчания этого мифа.

Увеличивать размер полимино бессмысленно, задачи по разрезанию от этого становятся проще и, как минимум, менее интересными. Зато достаточно любопытные вещи открываются, если вместо шахматной доски (8×8) в качестве базовой фигуры взять другой квадрат (или даже произвольный прямоугольник). Причём необязательно брать что-то большое. Достаточно квадрата 6×6.

Здесь увлекательно и достаточно содержательно обсудить возможность разбиения квадрата на тетрамино. Попытки нарисовать картинку приводят к тому, что возможно разбить на 9 квадратных тетрамино. На косые, как мы уже обсудили выше, нельзя разбить никакую доску. С остальными тоже не выходит: постоянно остаются хотя бы 4 свободные клетки. Младшие школьники пытаются сформулировать своё доказательство, по аналогии с делимостью площади: «раз всегда остаётся 4 клетки, значит разрезать нельзя». Однако, что значит «всегда»? Один, два раза, может быть пять раз попробовали нарисовать картинку? Это не аргумент.

Конечно, существует полный перебор (и для доски 6×6 он даже не вызывает острого желания воспользоваться помощью компьютера), но это не самое удовлетворительное решение. Как же быть?

Докажем, что доску 6×6 невозможно разделить на T-тетрамино. Для этого представим, что наша доска – часть обычной шахматной, то есть все её клетки покрашены в чёрный и белый цвета.

Рисунок 12. «Шахматная» доска 6×6

Заметим, что клеток каждого цвета на доске по 18, а каждое T-тетрамино, которое мы можем вырезать из неё содержит три клетки одного цвета и одну клетку другого.

Рисунок 13. T-тетрамино на шахматной доске