Марат Авдыев - Восхождение к вершине гиперкуба. Великая теорема Ферма для миллиардов обычных людей

– А нельзя ли было «заключить пари» на какую-нибудь более простую теорему, например очередное геометрическое доказательство теоремы Пифагора? – улыбаясь спросил Борщов ….

– Александр Николаевич, – вступила в разговор Татьяна Кузнецова, теперь это уже поздно. Если Матвей пойдёт на попятную, то Гангрена всё равно добьется его отчисления, вернее сделает так, что Матвей сам захочет «чтобы его ушли», то есть «уволили по собственному желанию». Мы так хотим этого не допустить, и готовы разыграть свой шанс, даже если счастливый билет – лишь один на миллион.

– Да, как мне это напоминает мир взрослых, – с сожалением задумчиво заметил Борщов, – и чем я могу Вам помочь? Ведь если я стану заниматься подсказками, то Ваш спор или пари будет считаться нечестным. Вместе с тем, если Вы, Татьяна, признаетесь Генриетте Григорьевне, что помогали Матвею, потому что Теорема очень трудная, сотни и сотни маститых математиков, как говорится, «обломали себе зубы» в поисках решения, то я уверен, что даже самые консервативные преподаватели поддержат Матвея. Если не ошибаюсь, в в 1994 году профессор математики Эндрю Уайлс отыскал доказательство на 140—150 страниц. Вы представляете теперь, насколько это сложно?

– А что если Пьер де Ферма был прав, утверждая, что существует простоте краткое решение, о котором он упоминал на полях Арифметики Диофанта? – уверенно возразил Матвей.

– Если он не хвастал, то нам остаётся лишь включить творческое воображение и воссоздать это поистине чудесное решение! – продолжила Татьяна. Она увлекалась книгами по психологии, самопознанию и часто читала популярную литературу о лидерстве.

– Хорошо, сказал Борщов. Я помогу Вам но не в роли преподавателя, а скорее в качестве фасилитатора , то есть, создающего общие условия научного поиска, но решение, если оно существует, будет только Вашим решением. Если Вы его не найдёте, то бескомпромиссно выполните требования Генриетты Григорьевны, какими бы «драконовскими» они Вам не представлялись, и при этом, как говорится, без слёз и соплей, то есть не будете давить на жалость. Идёт? – профессор Борщов замолчал и пристально посмотрел на Матвея с Татьяной.

Сейчас его взгляд был суровым, как с доски Наша ревизионная комиссия : те же усы, та же полированная лысина (не хватает лишь нагана для полного комплекта так, на всякий случай! Шутили университетские студенты и физматшкольники). При этом эта революционная внешность совсем не вязалась с мягким негромким голосом Борщова, его робостью, с которой он всякий раз входил в аудиторию, тщательно перепроверяя, не ошибся ли он дверью.

– Идёт, ответили ребята.

– Мы знаем, в каком направлении искать, сказал Матвей. Если Пьер де Ферма упомянул о сильном озарении, посетившем его, то скорее всего, решение может быть в виде рисунка, чертежа с минимальным количеством формул, как в Олимпиадной задаче. Просто раньше математики искали доказательство не в том направлении.

Борщов многозначительно кивнул и указал на часы. Ребята поспешно удались.

Не меняя общности, можно считать что справедливо неравенство для нашей тройки чисел a

Рис. 1.1. Целые числа a, b, c будут обязательно разные Доказательство от противного

Слагаемые a, b не могут быть равными, в силу иррациональности числа √2, которое невозможно представить в виде дроби, состоящей из не имеющих общих делителей числителя и знаменателя p и q.

Числа натуральные, целые, рациональные, иррациональные и трансцендентальные.

Напомним, что в начальных классах школы на уроках арифметики изучаются натуральные числа: 1,2,3,4,5…, которые используются, например для счёта предметов. Говорят, что такие числа образуют бесконечное множество N. Оно обозначается фигурными скобками N = {1,2,3,4,5 ….}. Каким бы большим не было натуральное число n, всегда найдётся число на единицу больше n+1. Конечно, это математическое упрощение, физики установили, что даже Вселенная имеет конечные размеры, определяемое как скорость света с = 3*10 8 м/с умножить на 15 млрд лет. (Любознательные могут рассчитать размер Вселенной в метрах, для чего удобно принять во внимание, что в году примерно π *10 7 секунд). Оказалось, что для вычислений очень удобно работать с целыми числами, где наряду с положительными имеются также ноль и отрицательные числа. Кольцо целых чисел Z =… -3, -2, -1,0,1,2,3 … с операциями слоения вычитания и умножения. Но и целых чисел не достаточно было для решения задач аграрной индустрии, архитектуры, торговли и мануфактуры, промышленности: именно эти отрасли знаний стимулировали развитие математики. Ещё в Древней Греции были открыты рациональные, иррациональные и трансцендентные числа, впоследствии математики дали им строгое определение.

Рациональное числа представляются в виде дроби p/q. Можно сократить числитель и знаменатель до взаимно простых чисел, разделив их на НОД – наибольший общий делитель. Например, вместо 4/6 писать 2/3. Целую часть можно записать рядом с дробной как-то: 3/2 =1 ½.

Если читать умеет делить числа в столбик, то сможет дробное представление числа привести к десятичному виду, как например 2/3 = 0,6666666666…, рано или поздно в этом ряду появится повторение одной или последовательности цифр или одной и той же цифры. Это происходит потому, что остаток от деления чисел всегда делится на одно и то же делимое. Рано или поздно варианты разных остатков будут исчерпаны и начнётся циклическое повторением (математики вводят понятие сравнение чисел по модулю, принцип Дирихле, а можно просто поэкспериментировать самостоятельно и убедиться!)

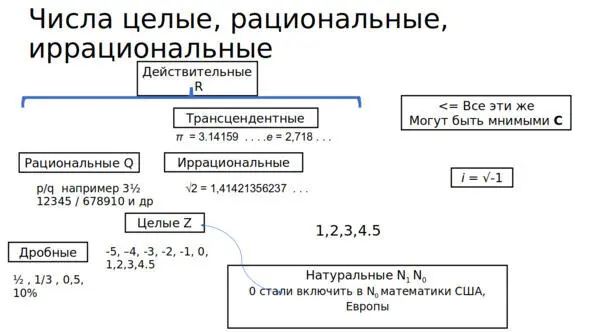
Рис. 1.2. Числа.

Вместе с тем, наряду с рациональными существуют иррациональные числа, они не могут быть представлены в виде десятичной дроби с повторяющейся последовательностью чисел, как например, √2= 1.41…. является иррациональным числом. Допустим обратное, которое представимо в виде дроби, состоящей из не имеющих общих делителей числителя и знаменателя p и q. Рассмотрим внимательнее уравнение 2q 2= p 2Его левая часть делится на два, значит правая часть делится уже на четыре, поскольку p можно разложить на простые числа, как то: 2,3,5,7,11,13,17 …. делящиеся только на себя и на единицу. Набор сомножителей в правой части будет повторяться дважды для p 2, отсюда свойство делимости на четыре. Но тогда в этом уравнении и q будет делиться на два. Смело сократив левую часть на общий делитель два в итоге получим что числа p и q, вопреки сделанному допущению, имеют в качестве общего делителя двойку и её степени. А это означает, что исходное предложение относительно числителя и знаменателя оказалось ошибочным: оба они четные, делятся на два, но мы исходно предполагали, что p, q не имеют общих делителей, которые заранее сократили. Значит √2 не представляется в виде дроби, аналогичные рассуждения применимы для корня из двух степени n.